题目内容
已知一个三角形的三边长构成等比数列,其公比为 ,则函数
,则函数 =
= -
- 的值域为
的值域为
 ,则函数
,则函数 =
= -
- 的值域为
的值域为A.( ,+∞) ,+∞) | B.[ ,+∞) ,+∞) | C.( ,-1) ,-1) | D.[ ,-1) ,-1) |
D
分析:由题意先设出三边为a、xa、x2a、x>0则由三边关系:两短边和大于第三边a+b>c,分公比大于1与公式在小于1两类解出公比的取值范围,此两者的并集是函数y=x2-
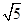 x的定义域,再由二次函数的性质求出它的值域,选出正确选项.
x的定义域,再由二次函数的性质求出它的值域,选出正确选项.解:设三边:a、xa、x2a、x>0则由三边关系:两短边和大于第三边a+b>c,即
(1)当x≥1时a+ax>ax2,等价于解二次不等式:x2-x-1<0,由于方程x2-x-1=0两根为:
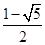 和
和 ,
,故得解:
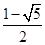 <q<
<q< 且x≥1,
且x≥1,即1≤x<

(2)当x<1时,a为最大边,xa+x2a>a即得x2+x-1>0,解之得x>
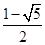 或x<-
或x<- 且x>0
且x>0即x>

综合(1)(2),得:x∈(
 ,
, )
)又y=x2-
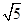 x的对称轴是x=
x的对称轴是x=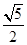 ,故函数在(
,故函数在( ,
,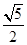 )是减函数,在(
)是减函数,在(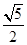 ,
, )是增函数
)是增函数由于x=
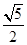 时,y=-
时,y=- ;x=
;x= 与x=
与x= 时,y=-1
时,y=-1所以函数y=x2-
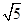 x的值域为[-
x的值域为[- ,-1)
,-1)观察四个选项知应选D
故选D

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
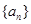 为等比数列,且满足
为等比数列,且满足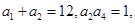 则
则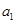 =( )
=( )
 或16
或16 中,已知
中,已知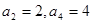 ,则
,则
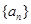 中,
中,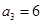 ,前三项和
,前三项和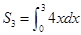 ,则公比q的值为 ( )
,则公比q的值为 ( )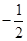
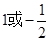
 的公比
的公比 ,前
,前 项和为
项和为 ,则
,则 。
。
