题目内容
已知圆![]() 方程为:
方程为:![]() .
.
(1)直线![]() 过点
过点![]() ,且与圆
,且与圆![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)过圆![]() 上一动点
上一动点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() ,设
,设![]() 与
与![]() 轴的交点为
轴的交点为![]() ,若向量
,若向量![]() ,求动点
,求动点![]() 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
(1)所求直线方程为 ![]() (2)轨迹是中心在原点,焦点在
(2)轨迹是中心在原点,焦点在![]() 轴,长轴为
轴,长轴为![]() 、短轴为
、短轴为![]() 的椭圆,除去短轴端点
的椭圆,除去短轴端点
解析:
(1)①当直线![]() 垂直于
垂直于![]() 轴时,则此时直线方程为
轴时,则此时直线方程为![]() ,
,![]() 与圆的两个交点坐标为
与圆的两个交点坐标为![]() 和
和![]() ,其距离为
,其距离为![]() 满足题意 …………………………………1分
满足题意 …………………………………1分
②若直线![]() 不垂直于
不垂直于![]() 轴,设其方程为
轴,设其方程为![]() ,即
,即![]()
设圆心到此直线的距离为![]() ,则
,则![]() ,得
,得![]() …………………3分
…………………3分
∴![]() ,解得
,解得![]() ,………………5分
,………………5分
故所求直线方程为 ![]() …………6分
…………6分
综上所述,所求直线方程为![]() 或
或![]() ……………………………7分
……………………………7分
(2)设点![]() 的坐标为
的坐标为![]() ,
,![]() 点坐标为
点坐标为![]() ,则
,则![]() 点坐标
点坐标
是![]() ……9分
……9分
∵![]() ,∴
,∴![]() 即
即![]() ,
,
![]() …………………11分
…………………11分
又∵![]() ,∴
,∴![]()
∴![]() 点的轨迹方程是
点的轨迹方程是![]() , ………………13分
, ………………13分
轨迹是中心在原点,焦点在![]() 轴,长轴为
轴,长轴为![]() 、短轴为
、短轴为![]() 的椭圆,除去短轴端点。…14分
的椭圆,除去短轴端点。…14分

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
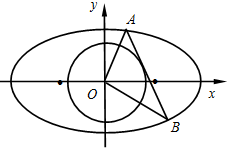 已知
已知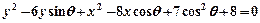 。
。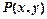 是(1)中曲线C上的动点,求
是(1)中曲线C上的动点,求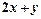 的取值范围。
的取值范围。 方程为:
方程为: .
. 过点
过点 ,且与圆
,且与圆 、
、 两点,若
两点,若 ,求直线
,求直线 作平行于
作平行于 轴的直线
轴的直线 ,设
,设 轴的交点为
轴的交点为 ,若向量
,若向量 ,求动点
,求动点 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.