题目内容
已知圆方程为:x2+y2=4.
(Ⅰ)直线L过点P(1,2),且与圆C交于A、B两点,若|AB|=2
,求直线L方程.
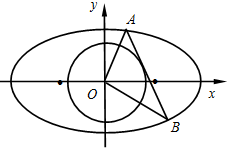
(Ⅱ)过圆C上一动点M作平行于X轴的直线m,设m与y轴交点为N,若向量
=
+
(O为原点),求动点Q轨迹方程.
(Ⅰ)直线L过点P(1,2),且与圆C交于A、B两点,若|AB|=2
| 3 |
(Ⅱ)过圆C上一动点M作平行于X轴的直线m,设m与y轴交点为N,若向量
| OQ |
| OM |
| ON |
分析:(I)分类讨论:直线L的斜率不存在时,方程为x=1,直接解出看是否满足|AB|=2
即可.当直线L的斜率存在时,设直线L的斜率为,则方程为:y-2=k(x-1),利用点到直线的距离距离公式可得圆心到直线L的距离d,利用弦长公式可得|AB|=2
,即可得到k.
(II)设Q(x,y),M(s,t),则N(0,t),由于向量
=
+
(O为原点),利用向量相等可得
,解出s,t再代入圆的方程即可.
| 3 |
| r2-d2 |
(II)设Q(x,y),M(s,t),则N(0,t),由于向量
| OQ |
| OM |
| ON |
|
解答:解:(I)①直线L的斜率不存在时,方程为x=1,代入圆的方程:1+y2=4,解得y=±
,满足|AB|=2
,此时:直线L的方程为,x=1.
②直线L的斜率存在时,设直线L的斜率为,则方程为:y-2=k(x-1),kx-y+2-k=0.
圆心到直线L的距离d=
,
∵|AB|=2
,∴2
=2
,
∴
=
,化为4k=3,解得k=
,
此时方程为:
x-y+2-
=0,化为3x-4y+5=0.
综上可知:直线L的方程为x=1或3x-4y+5=0.
(II)设Q(x,y),M(s,t),则N(0,t),s2+t2=4.(*)
∵向量
=
+
(O为原点),∴
,
解得
,代入(*)得x2+
=4,化为
+
=1.
因此动点Q轨迹方程为:
+
=1.
| 3 |
| 3 |
②直线L的斜率存在时,设直线L的斜率为,则方程为:y-2=k(x-1),kx-y+2-k=0.
圆心到直线L的距离d=
| |2-k| | ||
|
∵|AB|=2
| 3 |
| 3 |
| r2-d2 |
∴
| 3 |
4-(
|
| 3 |
| 4 |
此时方程为:
| 3 |
| 4 |
| 3 |
| 4 |
综上可知:直线L的方程为x=1或3x-4y+5=0.
(II)设Q(x,y),M(s,t),则N(0,t),s2+t2=4.(*)
∵向量
| OQ |
| OM |
| ON |
|
解得
|
| y2 |
| 4 |
| x2 |
| 4 |
| y2 |
| 16 |
因此动点Q轨迹方程为:
| x2 |
| 4 |
| y2 |
| 16 |
点评:本题考查了直线与圆相交的弦长问题、弦长公式、点到直线的距离公式、“代点法”、分类讨论等基础知识与基本技能方法,属于中档题.

练习册系列答案
相关题目
 已知
已知