题目内容
已知| OA |
| x |
| 3 |
| 3 |
| x |
| 3 |
| OB |
| x |
| 3 |
| x |
| 3 |
| OA |
| OB |
（1）求函数f（x）图象的对称中心的横坐标
（2）若x∈(0，
| π |
| 3 |
分析：（1）根据所给的向量的坐标，表示出两个向量的数量积的运算，根据三角函数的恒等变形，整理出最简形式，使得函数中对应的角等于正弦函数的对称中心的横标，得到结果．
（2）根据所给的变量x的值，依次写出函数的角度对应的区间，根据正弦曲线写出正弦函数的结果．
（2）根据所给的变量x的值，依次写出函数的角度对应的区间，根据正弦曲线写出正弦函数的结果．
解答：解：∵
=(sin
，
cos
)，
=(cos
，cos
)
f(x)=
•
=sin
cos
+
cos
cos
=sin（
+
）+
（1）
+
=kπ，
∴x=
-
，（k∈z）
∴f（x）图象的对称中心是（
-
，
）
（2）∵x∈(0，
]，
∴
＜
+
≤
∴
＜sin（
+
）≤1
∴f（x）d的值域是（
，1+
]
| OA |
| x |
| 3 |
| 3 |
| x |
| 3 |
| OB |
| x |
| 3 |
| x |
| 3 |
f(x)=
| OA |
| OB |
| x |
| 3 |
| x |
| 3 |
| 3 |
| x |
| 3 |
| x |
| 3 |
=sin（
| 2x |
| 3 |
| π |
| 3 |
| ||
| 2 |
（1）
| 3kπ |
| 2 |
| π |
| 3 |
∴x=
| 3kπ |
| 2 |
| π |
| 2 |
∴f（x）图象的对称中心是（
| 3kπ |
| 2 |
| π |
| 2 |
| ||
| 2 |
（2）∵x∈(0，
| π |
| 3 |
∴
| π |
| 3 |
| 2x |
| 3 |
| π |
| 3 |
| 5π |
| 9 |
∴
| ||
| 2 |
| 2x |
| 3 |
| π |
| 3 |
∴f（x）d的值域是（
| 3 |
| ||
| 2 |
点评：本题考查三角函数的恒等变换，本题解题的关键是对函数式进行整理，只有整理正确函数式，后面的关于正弦函数的性质的运算才能有正确结果．
练习册系列答案
相关题目
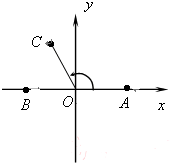在如图所示的平面直角坐标系中，已知点．A（1，0）和点B（-1，0），