题目内容
已知定点A（4，0）到等轴双曲线x2-y2=a2（a＞0）上的点的最近距离为
，求此双曲线的方程，并求此双曲线上到点A的距离为
的点的坐标．
| 5 |
| 5 |
分析：设点P（x，y）是双曲线x2-y2=a2上任意一点，表示出双曲线上到点A的距离，配方，分类讨论，可求双曲线的方程．
解答：解：设点P（x，y）是双曲线x2-y2=a2上任意一点，
则|AP|2=（x-4）2+y2=（x-4）2+（x2-a2）=2（x-2）2+8-a2
∵|x|≥a，
∴（1）当0＜a≤2时，
在x=2时，|AP
=8-a2=5，
∴a2=3，a=
，
此时双曲线方程为x2-y2=3，
双曲线上离A距离为
的点为（2，1）或（2，-1）
（2）当a＞2时，在x=a时，|AP
=2(a-2)2+8-a2=5，
∴a=4+
．
此时双曲线方程为x2-y2=21+8
，
双曲线上离A距离为
的点的坐标为(4+
，0)．
则|AP|2=（x-4）2+y2=（x-4）2+（x2-a2）=2（x-2）2+8-a2
∵|x|≥a，
∴（1）当0＜a≤2时，
在x=2时，|AP
| | | 2 min |
∴a2=3，a=
| 3 |
此时双曲线方程为x2-y2=3，
双曲线上离A距离为
| 5 |
（2）当a＞2时，在x=a时，|AP
| | | 2 min |
∴a=4+
| 5 |
此时双曲线方程为x2-y2=21+8
| 5 |
双曲线上离A距离为
| 5 |
| 5 |
点评：本题考查双曲线的标准方程，考查分类讨论的数学思想，考查学生的计算能力，属于中档题．
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
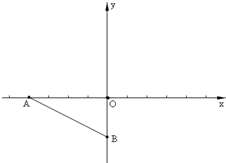在平面直角坐标系xOy中，已知定点A（-4，0），B（0，-2），半径为r的圆M的圆心M在线段AB的垂直平分线上，且在y轴右侧，圆M被y轴截得的弦长为
。
。