题目内容
(本小题满分12分)
已知直线 :
:
 和椭圆
和椭圆 ,椭圆C的离心率为
,椭圆C的离心率为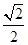 ,连结椭圆的四个顶点形成四边形的面积为
,连结椭圆的四个顶点形成四边形的面积为 .
.
(1)求椭圆C的方程;
(2)若直线 与椭圆C有两个不同的交点,求实数m的取值范围;
与椭圆C有两个不同的交点,求实数m的取值范围;
(3)当 时,设直线
时,设直线 与y轴的交点为P,M为椭圆C上的动点,求线段PM长度的最大值.
与y轴的交点为P,M为椭圆C上的动点,求线段PM长度的最大值.
已知直线
 :
:
 和椭圆
和椭圆 ,椭圆C的离心率为
,椭圆C的离心率为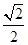 ,连结椭圆的四个顶点形成四边形的面积为
,连结椭圆的四个顶点形成四边形的面积为 .
.(1)求椭圆C的方程;
(2)若直线
 与椭圆C有两个不同的交点,求实数m的取值范围;
与椭圆C有两个不同的交点,求实数m的取值范围;(3)当
 时,设直线
时,设直线 与y轴的交点为P,M为椭圆C上的动点,求线段PM长度的最大值.
与y轴的交点为P,M为椭圆C上的动点,求线段PM长度的最大值.(1)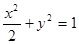 ;(2)
;(2)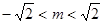 ;(3)|
;(3)|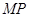 |取得最大值
|取得最大值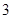 .
.
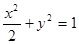 ;(2)
;(2)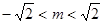 ;(3)|
;(3)|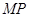 |取得最大值
|取得最大值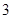 .
.试题分析:本题主要考查椭圆的标准方程、直线与椭圆的相交问题、两点间的距离公式、配方法求函数最值等基础知识,考查学生的分析问题解决问题的能力、计算能力.第一问,利用椭圆的标准方程,利用离心率求出基本量a和b,从而得到椭圆的标准方程;第二问,直线与椭圆方程联立,消参,由于直线与椭圆交于2个点,所以消参后的方程的判别式大于0,解不等式求出m的取值范围;第三问,将m=2代入,直接得到直线
 的方程,从而得到p点坐标,设出p点坐标,则利用两点间距离公式可求出
的方程,从而得到p点坐标,设出p点坐标,则利用两点间距离公式可求出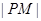 ,利用点M在椭圆上,转化x,通过配方法求函数的最值.
,利用点M在椭圆上,转化x,通过配方法求函数的最值.(1)由离心率
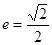 ,得
,得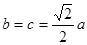
又因为
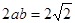 ,所以
,所以 ,
,即椭圆标准方程为
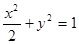 . 4分
. 4分(2)由
 消
消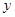 得:
得: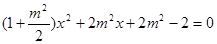 .
.所以
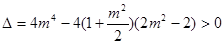 , 可化为
, 可化为 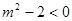
解得
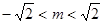 . 8分
. 8分(3)由l:
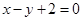 ,设
,设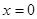 , 则
, 则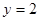 , 所以
, 所以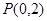 9分
9分设
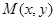 满足
满足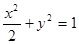 ,
,则
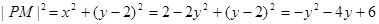 |
|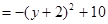
因为
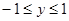 , 所以 11分
, 所以 11分当
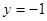 时,|
时,|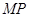 |取得最大值
|取得最大值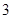 . 12分
. 12分
练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
 (
(  )的离心率为
)的离心率为 ,点(1,
,点(1, )在椭圆C上.
)在椭圆C上.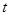 ),其中
),其中 ,切点分别是A、B,试利用结论:在椭圆
,切点分别是A、B,试利用结论:在椭圆 )处的椭圆切线方程是
)处的椭圆切线方程是 ,证明直线AB恒过椭圆的右焦点
,证明直线AB恒过椭圆的右焦点 ;
;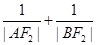 的值是否恒为常数,若是,求出此常数;若不是,请说明理由.
的值是否恒为常数,若是,求出此常数;若不是,请说明理由.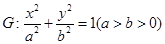 过点
过点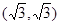 ,且离心率为
,且离心率为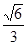 .斜率为
.斜率为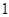 的直线
的直线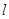 与椭圆
与椭圆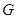 交于
交于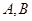 两点,以
两点,以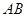 为底边作等腰三角形,顶点为
为底边作等腰三角形,顶点为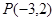 .
.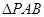 的面积.
的面积. :
: 的左顶点为
的左顶点为 ,直线
,直线 交椭圆
交椭圆 两点(
两点( 上
上 下),动点
下),动点 和定点
和定点 都在椭圆
都在椭圆 的面积.
的面积. 为梯形,求点
为梯形,求点 为实数,
为实数, ,求
,求 的取值范围.
的取值范围.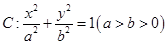 的左、右焦点分别为
的左、右焦点分别为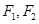 ,上顶点为A,在x轴负半轴上有一点B,满足
,上顶点为A,在x轴负半轴上有一点B,满足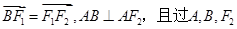 三点的圆与直线
三点的圆与直线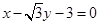 相切.
相切.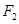 作斜率为k的直线
作斜率为k的直线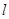 与椭圆C交于M,N两点,线段MN的垂直平分线与x轴相交于点P(m,0),求实数m的取值范围.
与椭圆C交于M,N两点,线段MN的垂直平分线与x轴相交于点P(m,0),求实数m的取值范围.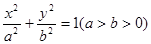 左右焦
左右焦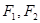 ,若椭圆C上恰有4个不同的点P,使得
,若椭圆C上恰有4个不同的点P,使得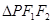 为等腰三角形,则C的离心率的取值范围是 _______
为等腰三角形,则C的离心率的取值范围是 _______ 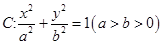 过点
过点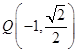 ,且离心率
,且离心率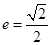 .
.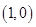 的直线
的直线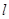 与该椭圆相交于A、B两点,试问:在直线
与该椭圆相交于A、B两点,试问:在直线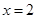 上是否存在点P,使得
上是否存在点P,使得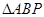 是正三角形?若存在,求出点P的坐标;若不存在,请说明理由.
是正三角形?若存在,求出点P的坐标;若不存在,请说明理由.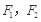 为焦点的椭圆上的一点,过焦点
为焦点的椭圆上的一点,过焦点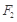 作
作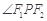 的外角平分线的垂线,垂足为M点,则点M的轨迹是( )
的外角平分线的垂线,垂足为M点,则点M的轨迹是( )