题目内容
3.已知函数y=$\frac{{x}^{2}-5x+a}{x-2}$(x>2,a>6)的最小值是5,求a的值.分析 x>2,a>6,变形函数y=$\frac{{x}^{2}-5x+a}{x-2}$=x-2+$\frac{a-6}{x-2}$-1,利用基本不等式的性质即可得出.
解答 解:∵x>2,a>6,
∴函数y=$\frac{{x}^{2}-5x+a}{x-2}$=$\frac{{x}^{2}-2x-3(x-2)+a-6}{x-2}$=x-2+$\frac{a-6}{x-2}$-1≥$2\sqrt{(x-2)•\frac{a-6}{x-2}}$-1=2$\sqrt{a-6}$-1,
当且仅当x-2=$\sqrt{a-6}$时,函数y=$\frac{{x}^{2}-5x+a}{x-2}$(x>2,a>6)的最小值2$\sqrt{a-6}$-1,
∴2$\sqrt{a-6}$-1=5,解得a=15.此时x=5.
∴a=15.
点评 本题考查了基本不等式的性质,考查了变形能力与计算能力,属于基础题.

练习册系列答案
相关题目
11.计算:$\frac{1-2si{n}^{2}α}{2co{s}^{2}α-1}$=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
18.平行四边形ABCD中,点P在边AB上(不含端点),$\overrightarrow{AP}=λ\overrightarrow{AB}$.若|$\overrightarrow{AP}$|=2,|$\overrightarrow{AD}$|=1,∠BAD=60°且$\overrightarrow{AP}•\overrightarrow{CP}$=-3.则λ=( )
| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
8.已知抛物线y2=2px(p>0)的焦点恰为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F2,双曲线C的左焦点为F1,若以F2为圆心的圆过点F1及双曲线C与该抛物线的交点,则双曲线C的离心率为( )
| A. | $\sqrt{2}$ | B. | 1+$\sqrt{2}$ | C. | 1+$\sqrt{3}$ | D. | 2+$\sqrt{3}$ |
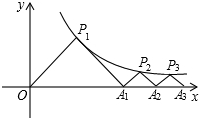 如图所示,P1(x1,y1)、P2(x2,y2),…Pn(xn,yn)在函数y=$\frac{4}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3…△PnAn-1An…都是等腰直角三角形,斜边OA1,A1A2…An-1An,都在x轴上,则y1+y2+…y10=$2\sqrt{10}$.
如图所示,P1(x1,y1)、P2(x2,y2),…Pn(xn,yn)在函数y=$\frac{4}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3…△PnAn-1An…都是等腰直角三角形,斜边OA1,A1A2…An-1An,都在x轴上,则y1+y2+…y10=$2\sqrt{10}$.