题目内容
18.(1)求值:lg5•lg400+(lg2${\;}^{\sqrt{2}}$)2;(2)已知x=log23,求$\frac{{8}^{x}+{8}^{-x}}{{2}^{x}+{2}^{-x}}$的值.
分析 (1)直接利用对数的运算性质化简求值;
(2)把x=log23代入$\frac{{8}^{x}+{8}^{-x}}{{2}^{x}+{2}^{-x}}$,然后利用对数的运算性质结合有理指数幂的运算性质化简得答案.
解答 解:(1)lg5•lg400+(lg2${\;}^{\sqrt{2}}$)2
=lg5(lg4+lg100)+$(\sqrt{2}lg2)^{2}$
=2lg5•lg2+2lg5+2lg22
=2lg2(lg5+lg2)+2lg5
=2lg2+2lg5
=2(lg5+lg2)
=2;
(2)∵x=log23,
∴$\frac{{8}^{x}+{8}^{-x}}{{2}^{x}+{2}^{-x}}$=$\frac{{8}^{lo{g}_{2}3}+{8}^{-lo{g}_{2}3}}{{2}^{lo{g}_{2}3}+{2}^{-lo{g}_{2}3}}$
=$\frac{({2}^{lo{g}_{2}3})^{3}+({2}^{lo{g}_{2}\frac{1}{3}})^{3}}{3+\frac{1}{3}}$=$\frac{27+\frac{1}{27}}{3+\frac{1}{3}}=\frac{73}{9}$.
点评 本题考查有理指数幂的化简与求值,考查了对数的运算性质,是基础的计算题.

练习册系列答案
相关题目
8.已知长方体的底面是正方形,且边长为2,体对角线长为2$\sqrt{5}$,则它的表面积为( )
| A. | 4(3$\sqrt{3}$+4) | B. | 8(2$\sqrt{3}$+1) | C. | 12(2$\sqrt{3}$+1) | D. | 3($\sqrt{3}$+8) |
9.已知抛物线y2=12x上两点P(x1,y1)、Q(x2,y2),且x1+x2=8,则|PQ|的最大值为( )
| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
6.若一个底面是正三角形的三棱柱的正视图如图所示,则其体积等于( )
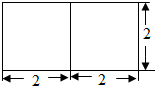

| A. | 2$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 8$\sqrt{3}$ | D. | 16$\sqrt{3}$ |