题目内容
(2008•嘉定区一模)函数f(x)=(sinx+cosx)cosx(x∈R)的最小正周期为
π
π
.分析:先利用乘法分配律给括号中各项都乘以cosx,然后分别利用二倍角的正弦、余弦函数公式进行化简,前两项提取
后,再利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,找出ω的值,代入周期公式T=
即可求出函数的最小正周期.
| ||
| 2 |
| 2π |
| ω |
解答:解:函数f(x)=(sinx+cosx)cosx
=sinxcosx+cos2x
=
sin2x+
(cos2x+1)
=
(sin2x+cos2x)+
=
sin(2x+
)+
,
∵ω=2,∴T=
=π.
故答案为:π
=sinxcosx+cos2x
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
∵ω=2,∴T=
| 2π |
| 2 |
故答案为:π
点评:此题考查了三角函数的周期性及其求法,涉及的知识有:二倍角的正弦、余弦函数公式,两角和与差的正弦函数公式,以及特殊角的三角函数值,其中利用三角函数的恒等变形把函数解析式化为一个角的三角函数是解本题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
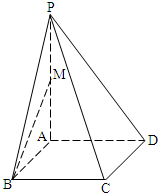 (2008•嘉定区一模)如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PA⊥平面ABCD,PC与平面ABCD所成角的大小为arctan2,M为PA的中点.
(2008•嘉定区一模)如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PA⊥平面ABCD,PC与平面ABCD所成角的大小为arctan2,M为PA的中点.