题目内容
(2008•嘉定区一模)定义在R上的函数f(x)满足f(x+2)=2f(x),当x∈[0,2]时,f(x)=x2-2x,则当x∈[-4,-2]时,函数f(x)的最小值为
-
| 1 |
| 4 |
-
.| 1 |
| 4 |
分析:定义在R上的函数f(x)满足f(x+2)=3f(x),可得出f(x-2)=13f(x),由此关系求出求出x∈[-4,-2]上的解析式,再配方求其最值.
解答:解:由题意定义在R上的函数f(x)满足f(x+2)=2f(x),
任取x∈[-4,-2],则f(x)=
f(x+2)=
f(x+4),
由于x+4∈[0,2],当x∈[0,2]时,f(x)=x2-2x,
故f(x)=
f(x+2)=
f(x+4)=
[(x+4)2-2(x+4)]=
(x2+6x+8)=
[(x+3)2-1],x∈[-4,-2]
当x=-3时,f(x)的最小值是-
.
故答案为:-
.
任取x∈[-4,-2],则f(x)=
| 1 |
| 2 |
| 1 |
| 4 |
由于x+4∈[0,2],当x∈[0,2]时,f(x)=x2-2x,
故f(x)=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
当x=-3时,f(x)的最小值是-
| 1 |
| 4 |
故答案为:-
| 1 |
| 4 |
点评:本题考查函数的最值及其几何意义,解题的关键是正确正解定义在R上的函数f(x)满足f(x+2)=2f(x),且由此关系求出x∈[-4,-2]上的解析式,做题时要善于利用恒恒等式.

练习册系列答案
相关题目
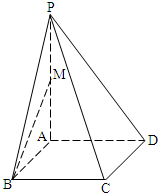 (2008•嘉定区一模)如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PA⊥平面ABCD,PC与平面ABCD所成角的大小为arctan2,M为PA的中点.
(2008•嘉定区一模)如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PA⊥平面ABCD,PC与平面ABCD所成角的大小为arctan2,M为PA的中点.