题目内容
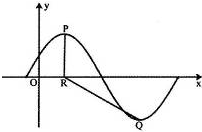 已知函数f(x)=Asin(
已知函数f(x)=Asin(| π |
| 6 |
| π |
| 2 |
| 2π |
| 3 |
分析:由题意直接求出函数的最大值A,通过点P的坐标为(2,A),点R的坐标为(2,0).若∠PRQ=
,画出图象,求出函数的周期,然后求出最大值,利用函数的图象经过P,求出?的值.
| 2π |
| 3 |
解答: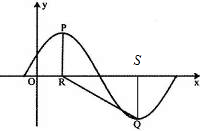 解:如图,
解:如图,
因为点P的坐标为(2,A),点R的坐标为(2,0).若∠PRQ=
,
所以∠SRQ=
-
=
.
SQ=A
RS=
=
=6,所以tan
=
=
=
,
A=2
.
P(2,2
),
所以2
=2
sin(
×2+?),解得?=2kπ+
-
,
k∈Z,
当k=0时,?=
.
故选A.
 解:如图,
解:如图,因为点P的坐标为(2,A),点R的坐标为(2,0).若∠PRQ=
| 2π |
| 3 |
所以∠SRQ=
| 2π |
| 3 |
| π |
| 2 |
| π |
| 6 |
SQ=A
RS=
| T |
| 2 |
| π | ||
|
| π |
| 6 |
| SQ |
| RS |
| A |
| 6 |
| ||
| 3 |
A=2
| 3 |
P(2,2
| 3 |
所以2
| 3 |
| 3 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
k∈Z,
当k=0时,?=
| π |
| 6 |
故选A.
点评:本题考查三角函数的解析式的求法,考查函数的图象的应用,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目