题目内容
下列命题中,不正确命题序号是
①圆(x+2)2+y2=4与圆(x-2)2+(y-1)2=9的位置关系为相交.
②框图一般按从上到下、从左到右的方向画.
③线性回归直线
=
x+
恒过样本中心(
,
).
④对立事件是互斥事件的特例.
⑤在面积为S的△ABC内任取一点P,记A=“△PBC的面积大于
”,则P(A)=
.
⑤
⑤
①圆(x+2)2+y2=4与圆(x-2)2+(y-1)2=9的位置关系为相交.
②框图一般按从上到下、从左到右的方向画.
③线性回归直线
 |
| y |
 |
| b |
 |
| a |
. |
| x |
. |
| y |
④对立事件是互斥事件的特例.
⑤在面积为S的△ABC内任取一点P,记A=“△PBC的面积大于
| S |
| 3 |
| 2 |
| 3 |
分析:①比较两圆心距与半径的大小;
②框图一般按从上到下、从左到右的方向画;
③线性回归直线恒过样本中心;
④两个事件是互斥事件,这两个事件不一定对立,但如果是对立事件,一定是互斥事件;
⑤首先分析题目求在面积为S的△ABC的边AB上任取一点P,要求△PBC的面积大于
的概率,即可考虑画图求解的方法,然后根据图形分析出基本的事件空间与事件的几何度量是什么.再根据几何关系求解出它们的比例即可.
②框图一般按从上到下、从左到右的方向画;
③线性回归直线恒过样本中心;
④两个事件是互斥事件,这两个事件不一定对立,但如果是对立事件,一定是互斥事件;
⑤首先分析题目求在面积为S的△ABC的边AB上任取一点P,要求△PBC的面积大于
| S |
| 3 |
解答: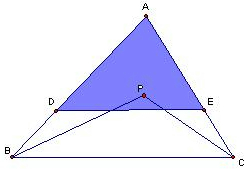 解:①由于
解:①由于
=
<2+3,
所以圆(x+2)2+y2=4与圆(x-2)2+(y-1)2=9的位置关系为相交,故①正确;
②框图一般按从上到下、从左到右的方向画,故②正确;
③线性回归直线
=
x+
恒过样本中心(
,
),故③正确;
④依据互斥、对立事件的定义,对立一定互斥而互斥不一定对立,则对立事件是互斥事件的特例,故④正确;
⑤记事件A={△PBC的面积大于
},
基本事件空间是三角形ABC的面积,(如图)
事件A的几何度量为图中阴影部分的面积(D、E分别是三角形的边上的三等分点),
因为△ADE∽△ABC,且相似比为
,
∴
=(
)2=
,
∴阴影部分的面积是整个三角形面积的
,
所以P(A)=
=
.故错
故答案为:⑤
 解:①由于
解:①由于| (2-(-2))2+(1-0)2 |
| 17 |
所以圆(x+2)2+y2=4与圆(x-2)2+(y-1)2=9的位置关系为相交,故①正确;
②框图一般按从上到下、从左到右的方向画,故②正确;
③线性回归直线
 |
| y |
 |
| b |
 |
| a |
. |
| x |
. |
| y |
④依据互斥、对立事件的定义,对立一定互斥而互斥不一定对立,则对立事件是互斥事件的特例,故④正确;
⑤记事件A={△PBC的面积大于
| S |
| 3 |
基本事件空间是三角形ABC的面积,(如图)
事件A的几何度量为图中阴影部分的面积(D、E分别是三角形的边上的三等分点),
因为△ADE∽△ABC,且相似比为
| 2 |
| 3 |
∴
| S△ADE |
| S△ABC |
| 2 |
| 3 |
| 4 |
| 9 |
∴阴影部分的面积是整个三角形面积的
| 4 |
| 9 |
所以P(A)=
| 阴影部分的面积 |
| 三角形ABC的面积 |
| 4 |
| 9 |
故答案为:⑤
点评:本题以命题的真假判断为载体,综合考查了统计与概率的有关知识,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目