题目内容
已知向量 ,
,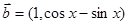 ,函数
,函数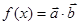 .
.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)在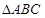 中,内角
中,内角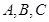 的对边分别为
的对边分别为 ,已知
,已知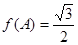 ,
,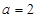 ,
,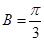 ,求
,求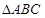 的面积
的面积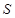 .
.
(1)函数 的单调递增区间为
的单调递增区间为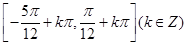 .(2)
.(2)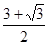 .
.
解析试题分析:(I)根据平面向量的数量积,应用和差倍半的三角函数公式,将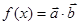 化简为
化简为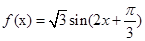 ,讨论函数的单调性;
,讨论函数的单调性;
(2)利用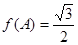 求得
求得 ,再应用正弦定理及两角和差的三角函数公式,求得
,再应用正弦定理及两角和差的三角函数公式,求得 ,应用三角形面积公式即得所求.
,应用三角形面积公式即得所求.
试题解析:
(1)
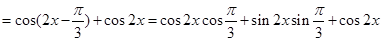
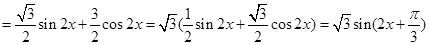 3分
3分
令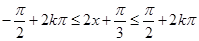 (
(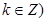 ,得
,得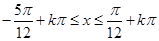 (
(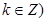 ,
,
所以,函数 的单调递增区间为
的单调递增区间为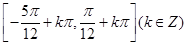 . 6分
. 6分
(2)由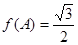 ,得
,得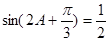 ,
,
因为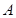 为
为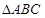 的内角,由题意知
的内角,由题意知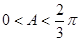 ,所以
,所以 ,
,
因此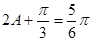 ,解得
,解得 , 8分
, 8分
又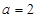 ,
,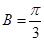 ,由正弦定理
,由正弦定理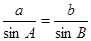 ,得
,得 , 10分
, 10分
由 ,
,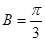 ,可得
,可得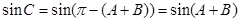

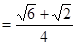 , 11分
, 11分
所以,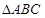 的面积
的面积
 =
=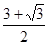 . 12分
. 12分
考点:平面向量的数量积,和差倍半的三角函数,正弦定理的应用,三角形面积公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
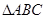 中,内角
中,内角 、
、 、
、 的对边分别为
的对边分别为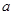 、
、 、
、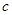 ,且
,且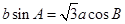 .
.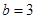 ,
, ,求
,求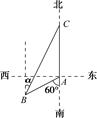
 ,点M在线段PQ上.
,点M在线段PQ上.
 ,求PM的长;
,求PM的长; .(1)求内角B的余弦值;(2)若
.(1)求内角B的余弦值;(2)若 ,求三角形
,求三角形 的面积.
的面积. 的图像经过点
的图像经过点 .
. 的值;
的值; 中,
中,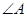 、
、 、
、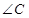 所对的边分别为
所对的边分别为 、
、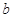 、
、 ,若
,若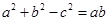 ,且
,且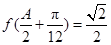 .求
.求 .
. 米(将眼睛S距地面的距离SA按
米(将眼睛S距地面的距离SA按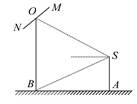

 中,角
中,角 所对的边分别为
所对的边分别为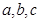 ,且,
,且, .
. 的值;
的值; ,
,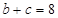 ,求三角形ABC的面积.
,求三角形ABC的面积.