题目内容
已知函数
（1）求
的最小正周期和单调递增区间；
（2）已知
是
三边长，且
,的面积
.求角
及
的值.
（1）求
的最小正周期和单调递增区间；（2）已知
是三边长，且,的面积.求角及的值.（1）
,
;（2）
或a=5,b=8.
,;（2）或a=5,b=8.试题分析：（2）由函数
的结构形式可得，应用正弦的和差的展开式公式，以及余弦的二倍角逆运算公式，将函数化简，再通过应用角和差的逆运算公式，将函数化简，即可求得最小正周期，和单调递增区间.（2）在三角形中，根据（Ⅰ）的结论，求出角C.又由已知面积、c边长这三个条件即可解三角形，及求出
的值.本小题在解关于的方程组时要用到整体的思想.试题解析：（Ⅰ）
,
，函数
的递增区间是（2）
或a=5,b=8
练习册系列答案
相关题目
.
的最小正周期；
．
的最小正周期；
上的最大值和最小值.
（
为常数且
），函数
在
上的最大值为
．
的值；
的图象向右平移
个单位，可得函数
的图象，若
上为增函数，求
，
，则
是（ ）
的奇函数
的奇函数
的导函数的图像如图所示，给出下列判断：
内单调递增；
内单调递减；
内单调递增；
时，函数
时，函数
的图象如图所示，则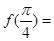
（ ）
sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
,
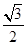),求f(θ)的值;
上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
的值域为 .