题目内容
求下列函数f(x)的解析式.
(1) 已知f(1-x)=2x2-x+1,求f(x);
(2) 已知f =x2+
=x2+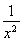 ,求f(x);
,求f(x);
(3) 已知一次函数f(x)满足f(f(x))=4x-1,求f(x);
(4) 定义在(-1,1)内的函数f(x)满足2f(x)-f(-x)=lg(x+1),求f(x).
(1)f(x)=2x2-3x+2(2)f(x)=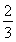 lg(x+1)+
lg(x+1)+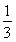 lg(1-x),x∈(-1,1).
lg(1-x),x∈(-1,1).
【解析】(1) (换元法)设t=1-x,则x=1-t,
∴ f(t)=2(1-t)2-(1-t)+1=2t2-3t+2,
∴ f(x)=2x2-3x+2.
(2) (配凑法)∵ f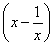 =x2+
=x2+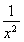 =
=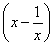 2+2,
2+2,
∴ f(x)=x2+2.
(3) (待定系数法)∵ f(x)是一次函数,∴设f(x)=ax+b(a≠0),则
f(f(x))=f(ax+b)=a(ax+b)+b=a2x+ab+b.
∵f(f(x))=4x-1,∴ 解得
解得 或
或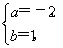
∴f(x)=2x-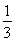 或f(x)=-2x+1.
或f(x)=-2x+1.
(4) (消去法)当x∈(-1,1)时,有2f(x)-f(-x)=lg(x+1),①
以-x代替x得2f(-x)-f(x)=lg(-x+1),②
由①②消去f(-x)得,f(x)=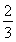 lg(x+1)+
lg(x+1)+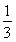 lg(1-x),x∈(-1,1)
lg(1-x),x∈(-1,1)

练习册系列答案
相关题目