题目内容
已知f(x)是定义在实数集R上的不恒为0的函数,对任意实数x,y有f(x)f(y)=f(x+y),当x>0时,有0<f(x)<1.
(Ⅰ)求f(0)的值,并证明f(x)恒正;
(Ⅱ)判断f(x)在实数集R上单调性;
(Ⅲ)设Sn为数列{an}的前n项和,a1= ,an=f(n)(n为正整数).令bn=f(Sn),问数列{bn}中是否存在最大项?若存在,求出最大项的值;若不存在,试说明理由.
,an=f(n)(n为正整数).令bn=f(Sn),问数列{bn}中是否存在最大项?若存在,求出最大项的值;若不存在,试说明理由.
解:(Ⅰ)由f(x)f(y)=f(x+y),令x>0,y=0,则f(x)f(0)=f(x),
∵当x>0时,有0<f(x)<1,∴f(0)=1.…
当x<0时,-x>0,∴0<f(-x)<1,
由于f(x)f(-x)=f(x-x)=f(0)=1
所以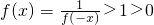 ,综上可知,f(x)恒正;…
,综上可知,f(x)恒正;…
(Ⅱ)设x1<x2,则x2-x1>0,∴0<f(x2-x1)<1
又由(1)可知f(x1)>0
所以f(x2)=f(x2-x1+x1)=f(x2-x1)f(x1)<f(x1)
故f(x)在实数集R上是减函数;…
(Ⅲ)由题意 ,an=f(n),
,an=f(n),
∴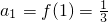 ,
,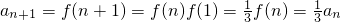
∴数列{an}为以首项 ,公比为
,公比为 的等比数列,
的等比数列,
∴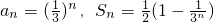 …
…
由此可知,Sn随着n的增大而增大,再根据(2)可得f(Sn)随着n的增大而减小,
所以数列{bn}为递减数列,
从而存在最大项,其为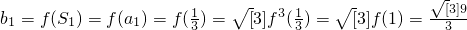 …
…
分析:(Ⅰ)由f(x)f(y)=f(x+y),利用赋值法,即可求f(0)的值,利用当x>0时,有0<f(x)<1,证明f(x)恒正;
(Ⅱ)利用函数单调性的定义,结合f(x)恒正,即可得到f(x)在实数集R上单调性;
(Ⅲ)确定数列{an}是通项与前n项和,可得可得f(Sn)随着n的增大而减小,从而数列{bn}为递减数列,由此可得结论.
点评:本题考查抽象函数,考查函数单调性的判断与证明,考查学生分析解决问题的能力,属于中档题.
∵当x>0时,有0<f(x)<1,∴f(0)=1.…
当x<0时,-x>0,∴0<f(-x)<1,
由于f(x)f(-x)=f(x-x)=f(0)=1
所以
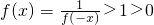 ,综上可知,f(x)恒正;…
,综上可知,f(x)恒正;…(Ⅱ)设x1<x2,则x2-x1>0,∴0<f(x2-x1)<1
又由(1)可知f(x1)>0
所以f(x2)=f(x2-x1+x1)=f(x2-x1)f(x1)<f(x1)
故f(x)在实数集R上是减函数;…
(Ⅲ)由题意
 ,an=f(n),
,an=f(n),∴
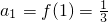 ,
,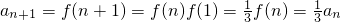
∴数列{an}为以首项
 ,公比为
,公比为 的等比数列,
的等比数列,∴
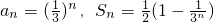 …
…由此可知,Sn随着n的增大而增大,再根据(2)可得f(Sn)随着n的增大而减小,
所以数列{bn}为递减数列,
从而存在最大项,其为
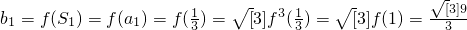 …
…分析:(Ⅰ)由f(x)f(y)=f(x+y),利用赋值法,即可求f(0)的值,利用当x>0时,有0<f(x)<1,证明f(x)恒正;
(Ⅱ)利用函数单调性的定义,结合f(x)恒正,即可得到f(x)在实数集R上单调性;
(Ⅲ)确定数列{an}是通项与前n项和,可得可得f(Sn)随着n的增大而减小,从而数列{bn}为递减数列,由此可得结论.
点评:本题考查抽象函数,考查函数单调性的判断与证明,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目