题目内容
(本小题满分12分)已知函数
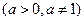 .
.
(1)求函数f(x)的定义域、值域;
(2)是否存在实数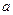 ,使得函数f(x
,使得函数f(x )满足:对于区间(2,+∞)上使函数f(x)有意义的一切x,都有f(x)≥0.
)满足:对于区间(2,+∞)上使函数f(x)有意义的一切x,都有f(x)≥0.

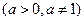 .
.(1)求函数f(x)的定义域、值域;
(2)是否存在实数
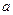 ,使得函数f(x
,使得函数f(x )满足:对于区间(2,+∞)上使函数f(x)有意义的一切x,都有f(x)≥0.
)满足:对于区间(2,+∞)上使函数f(x)有意义的一切x,都有f(x)≥0.解:(1)由4-ax≥0,得ax≤4.
当a>1时,x≤loga4; 当0<a<1时,x≥loga4.
即当a>1时,f(x)的定义域为(-∞,loga4];当0<a<1时,f(x)的定义域为[loga4,+∞).
令t= ,则0≤t<2,且ax=4-t2,?
,则0≤t<2,且ax=4-t2,?
∴f(x)=4-t2-2t-1=-(t+1)2+4, 当t≥0时,f(x)是t的单调减函数,
∴f(2)<f(x)≤f(0),即-5<f(x)≤3.∴函数f(x)的值域是(-5,3] .----------6分
(2)若存在实数a使得对于区间(2,+∞)上使函数f(x)有意义的一切x,都有?f(x)≥0,则区间(2,+∞)是定义域的子集.由(1)知,a>1不满足条件;若0<a<1,则loga4<2,且f(x)是x的减函数.
当x>2时,ax<a2.由于0<a2<1, ∴t=
∴f(x)<0,即f(x)≥0不成立 .
.
综上满足条件的a不存在. ------------------12分
当a>1时,x≤loga4; 当0<a<1时,x≥loga4.
即当a>1时,f(x)的定义域为(-∞,loga4];当0<a<1时,f(x)的定义域为[loga4,+∞).
令t=
 ,则0≤t<2,且ax=4-t2,?
,则0≤t<2,且ax=4-t2,?∴f(x)=4-t2-2t-1=-(t+1)2+4, 当t≥0时,f(x)是t的单调减函数,
∴f(2)<f(x)≤f(0),即-5<f(x)≤3.∴函数f(x)的值域是(-5,3] .----------6分
(2)若存在实数a使得对于区间(2,+∞)上使函数f(x)有意义的一切x,都有?f(x)≥0,则区间(2,+∞)是定义域的子集.由(1)知,a>1不满足条件;若0<a<1,则loga4<2,且f(x)是x的减函数.
当x>2时,ax<a2.由于0<a2<1, ∴t=

∴f(x)<0,即f(x)≥0不成立
 .
.综上满足条件的a不存在. ------------------12分
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,则a, b,c的大小关系是( )
,则a, b,c的大小关系是( ) 若f(f (1))=1,则a=________.
若f(f (1))=1,则a=________. 的图象过点(0,
的图象过点(0, ),且
),且 的解集为(1,3)。
的解集为(1,3)。 的解析式;
的解析式; ,
, 的最值。
的最值。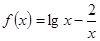 的零点所在的区间应是 ( )
的零点所在的区间应是 ( ) ,
, ,
, ,
, ,则函数
,则函数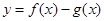 的零点个数为( )
的零点个数为( ) 上的函数
上的函数 ,满足
,满足 ,求证:函数
,求证:函数 在
在 上的可导函数,满足
上的可导函数,满足 ,则
,则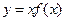 是
是 :
: ,若
,若  +
+
 ,
,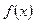 满足
满足 ,若
,若 ,则
,则 _______。
_______。 的定义域为_________
的定义域为_________