题目内容
(1)已知不等式ax2+bx+c>0的解集为{x|α<x<β,α∈R+},求不等式cx2+bx+a<0的解集.
(2)已知集合A={x|2x2+7x-15<0},B={x|x2+ax+b≤0},满足A∩B=![]() ,A∪B={x|-5<x≤2},求实数a,b的值.
,A∪B={x|-5<x≤2},求实数a,b的值.
答案:
解析:
解析:
|
思路 (1)已知一元二次不等式的解集,求二次三项式的系数,先判定系数的符号,再利用根与系数的关系即可求出. (2)化简集合A={x|-5<x< 解答 (1)方法1:∵原不等式的解为α<x<β, ∴a<0 由韦达定理,得α+β=- ∴αβx2-(α+β)x+1>0. 即(αx-1)(βx-1)>0 又β>α>0,∴ 故cx2+bx+a<0的解集为{x|x< 方法2:∵a<0, ∴x=0是cx2+bx+a<0的一个解. 当x≠0时,x2>0,对不等式cx2+bx+a<0两边同除以x2得: a·( ∵ax2+bx+c>0的解集为{x|α<x<β}. ∴(*)的解为 即x< 解集为{x|x< (2)A={x|2x2+7x-15<0}={x|-5<x<- ∵A∩B= ∴B={x| 故x2+ax+b≤0的解集为{x| 由(x- 评析 本题(1)体现了一元二次不等式与二次方程的联系,而不等式往往作为基本工具结合在其他知识之中,这体现了不等式知识的综合性. |

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
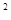 +bx+1<0的解集为{x|-1<x<2},则ab=
+bx+1<0的解集为{x|-1<x<2},则ab=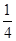 C.-
C.- D.1
D.1