题目内容
从区间(0,1)上任取两个实数a和b,则方程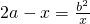 有实根的概率为
有实根的概率为
- A.

- B.

- C.

- D.

C
分析:方程x2-2ax+b2=0有实根,则判别式△=4(a2-b2)≥0.由于a2≥b2 和 a2<b2的概率相等,故判别式△≥0的概率等于 ,由此得出结论.
,由此得出结论.
解答:若方程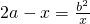 有实根,即x2-2ax+b2=0有实根,故判别式△=4(a2-b2)≥0.
有实根,即x2-2ax+b2=0有实根,故判别式△=4(a2-b2)≥0.
由于a2≥b2 和 a2<b2的概率相等,
故判别式△≥0的概率等于 ,
,
即方程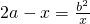 有实根的概率为
有实根的概率为  ,
,
故选C.
点评:本题主要考查等可能事件的概率,体现了转化的数学思想,属于基础题.
分析:方程x2-2ax+b2=0有实根,则判别式△=4(a2-b2)≥0.由于a2≥b2 和 a2<b2的概率相等,故判别式△≥0的概率等于
 ,由此得出结论.
,由此得出结论.解答:若方程
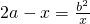 有实根,即x2-2ax+b2=0有实根,故判别式△=4(a2-b2)≥0.
有实根,即x2-2ax+b2=0有实根,故判别式△=4(a2-b2)≥0.由于a2≥b2 和 a2<b2的概率相等,
故判别式△≥0的概率等于
 ,
,即方程
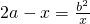 有实根的概率为
有实根的概率为  ,
,故选C.
点评:本题主要考查等可能事件的概率,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
从区间(0,1)上任取两个实数a和b,则方程2a-x=
有实根的概率为( )
| b |
| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
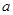 和
和 ,则方程
,则方程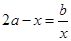 有实根的概率为( )
有实根的概率为( )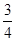 B.
B.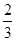 C.
C.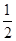 D.
D.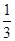
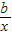 有实根的概率为( )
有实根的概率为( )



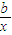 有实根的概率为( )
有实根的概率为( )


