题目内容
从区间(0,1)上任取两个实数a和b,则方程2a-x=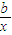 有实根的概率为( )
有实根的概率为( )A.

B.

C.

D.

【答案】分析:分别表示出从区间(0,1)上任取两个实数a和b,(a,b)点对应的平面区域D,及方程2a-x=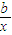 有实根的平面区域E,并分别求出D,E的面积,代入几何概型公式,即可得到答案.
有实根的平面区域E,并分别求出D,E的面积,代入几何概型公式,即可得到答案.
解答:解:从区间(0,1)上任取两个实数a和b,则(a,b)点对应的平面区域如下图中矩形所示:
若方程2a-x=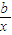 有实根,即x2-2ax+b=0有实根,
有实根,即x2-2ax+b=0有实根,
即△=4(a2-b)≥0,满足条件的平面区域如图中阴影部分所示
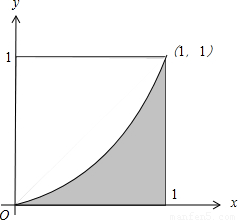
则S矩形=1,S阴影=∫1x2dx=
故方程2a-x=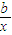 有实根的概率P=
有实根的概率P=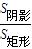 =
=
故选D
点评:本题考查的知识点是几何概型,其中求出所有基本事件对应的平面区域的面积,并利用定积分公式,求出满足条件的平面区域的面积,是解答本题的关键.
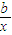 有实根的平面区域E,并分别求出D,E的面积,代入几何概型公式,即可得到答案.
有实根的平面区域E,并分别求出D,E的面积,代入几何概型公式,即可得到答案.解答:解:从区间(0,1)上任取两个实数a和b,则(a,b)点对应的平面区域如下图中矩形所示:
若方程2a-x=
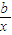 有实根,即x2-2ax+b=0有实根,
有实根,即x2-2ax+b=0有实根,即△=4(a2-b)≥0,满足条件的平面区域如图中阴影部分所示

则S矩形=1,S阴影=∫1x2dx=

故方程2a-x=
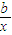 有实根的概率P=
有实根的概率P=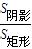 =
=
故选D
点评:本题考查的知识点是几何概型,其中求出所有基本事件对应的平面区域的面积,并利用定积分公式,求出满足条件的平面区域的面积,是解答本题的关键.

练习册系列答案
相关题目
从区间(0,1)上任取两个实数a和b,则方程2a-x=
有实根的概率为( )
| b |
| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
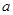 和
和 ,则方程
,则方程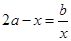 有实根的概率为( )
有实根的概率为( )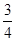 B.
B.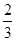 C.
C.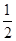 D.
D.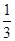
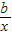 有实根的概率为( )
有实根的概率为( )


