题目内容
 设函数f(x)=
设函数f(x)=
|
(1)求函数f(x)的解析式;
(2)若f(x)=-1,求相应x的值;
(3)画出函数f(x)的图象,并说出函数f(x)的单调区间.
分析:(1)由f(-4)=f(0)和f(-2)=-1列出关于b、c的两个方程,求出b、c的值;
(2)根据(1)求出的解析式,分x≥0和x<0两种情况,分别求出x的值,注意验证范围.
(3)根据(1)求出的解析式,先画出函数的图象,根据图象写出函数的单调区间;
(2)根据(1)求出的解析式,分x≥0和x<0两种情况,分别求出x的值,注意验证范围.
(3)根据(1)求出的解析式,先画出函数的图象,根据图象写出函数的单调区间;
解答: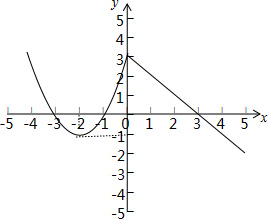 解:(1)∵f(-4)=f(0),f(-2)=-1,
解:(1)∵f(-4)=f(0),f(-2)=-1,
∴16-4b+c=3 ①,4-2b+c=-1 ②,
联立①②,解得:b=4,c=3
∴f(x)=
.
(2)当x≥0时,-x+3=-1,解得x=4;
当x<0时,x2+4x+3=-1,解得x=-2,
故x=4或-2;
(3)在坐标系中画出函数图象:
由图象可知单调区间为:(-∞,-2],(-2,0],(0,+∞),
其中增区间为(-2,0],减区间为(-∞,-2]和(0,+∞).
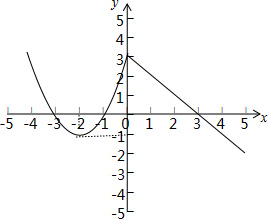 解:(1)∵f(-4)=f(0),f(-2)=-1,
解:(1)∵f(-4)=f(0),f(-2)=-1,∴16-4b+c=3 ①,4-2b+c=-1 ②,
联立①②,解得:b=4,c=3
∴f(x)=
|
(2)当x≥0时,-x+3=-1,解得x=4;
当x<0时,x2+4x+3=-1,解得x=-2,
故x=4或-2;
(3)在坐标系中画出函数图象:
由图象可知单调区间为:(-∞,-2],(-2,0],(0,+∞),
其中增区间为(-2,0],减区间为(-∞,-2]和(0,+∞).
点评:本题考查了函数的图象以及性质,利用函数值列方程求解析式中的系数,正确作函数的图象后,并且由图写出函数的单调区间,对于分段函数由函数值求自变量一定要分类代入对应的解析式求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 设函数
设函数 设函数
设函数