题目内容
 设函数f(x)=
设函数f(x)=
|
(1)求函数f(x)的解析式;
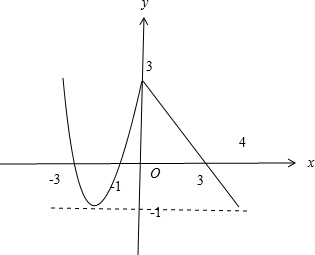
(2)画出函数f(x)的图象,并写出函数f(x)的定义域、值域.
分析:(1)由f(-4)=f(0),f(-2)=-1,可得b,c的关系,解方程可求b,c,进而可求f(x)
(2)根据每段函数的定义域可求出没段函数的值域,而分段函数的定义域、值域是每段函数的定义域与值域的并集可求
(2)根据每段函数的定义域可求出没段函数的值域,而分段函数的定义域、值域是每段函数的定义域与值域的并集可求
解答:解:(1)∵f(-4)=f(0),f(-2)=-1,
∴16-4b+c=3,4-2b+c=-1,
解得:b=4,c=3,
∴f(x)=
,
(2)函数的定义域为[-4,4],
当x<0时,y=x2+4x+3=(x+2)2-1
由x<0可得,y≥-1
当x≥0时,y=-x+3≤3
∴-1≤y≤3
∴函数的值域为[-1,3].其图象如图所示
∴16-4b+c=3,4-2b+c=-1,
解得:b=4,c=3,
∴f(x)=
|
(2)函数的定义域为[-4,4],
当x<0时,y=x2+4x+3=(x+2)2-1
由x<0可得,y≥-1
当x≥0时,y=-x+3≤3
∴-1≤y≤3
∴函数的值域为[-1,3].其图象如图所示

点评:本题主要考查了分段函数的函数解析式的求解,解题时一定要注意每段函数的函数的定义域,分段函数的函数定义域与值域的求解,属于基础试题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 设函数
设函数