题目内容
 设函数f(x)=
设函数f(x)=
|
(1)求函数f(x)的解析式;
(2)画出函数f(x)的图象,并指出函数f(x)的单调区间.
(3)若方程f(x)=k有两个不等的实数根,求k的值.
分析:(1)由函数f(x)=
,且f(-4)=f(0),f(-2)=-1,能推导出b=4,c=3.由此能求出f(x).
(2)由f(x)=
,知:当x<0时,f(x)的图象是开口向上,对称轴为x=-2的抛物线,当x≥0时,f(x)的图象是一条直线,由此能求出f(x)的图象.
(3)由方程f(x)=k有两个不等的实数根,知x2+4x+3=k(x<0)有两个不等的实数根,由此能求出k的取值范围.
|
(2)由f(x)=
|
(3)由方程f(x)=k有两个不等的实数根,知x2+4x+3=k(x<0)有两个不等的实数根,由此能求出k的取值范围.
解答:解:(1)∵函数f(x)=
,
且f(-4)=f(0),f(-2)=-1,
∴
,解得b=4,c=3.
∴f(x)=
.
(2)∵f(x)=
,
∴当x<0时,f(x)的图象是开口向上,对称轴为x=-2的抛物线,
当x≥0时,f(x)的图象是一条直线.
列表
描点,连线,得到f(x)的图象:
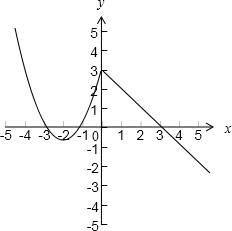
(3)∵方程f(x)=k有两个不等的实数根,
∴x2+4x+3=k(x<0)有两个不等的实数根,
∴
,
解得-
<k<3.
故k的取值范围是(-
,3).
|
且f(-4)=f(0),f(-2)=-1,
∴
|
∴f(x)=
|
(2)∵f(x)=
|
∴当x<0时,f(x)的图象是开口向上,对称轴为x=-2的抛物线,
当x≥0时,f(x)的图象是一条直线.
列表
| x | … | -4 | -3 | -2 | -1 | 0 | 1 | … |
| f(x) | … | 3 | 0 | -1 | 0 | 3 | 2 | … |

(3)∵方程f(x)=k有两个不等的实数根,
∴x2+4x+3=k(x<0)有两个不等的实数根,
∴
|
解得-
| 4 |
| 3 |
故k的取值范围是(-
| 4 |
| 3 |
点评:本题考果函数的解析式的求法,考查函数的图象的作法,考查实数的取值范围的求法.易错点是容易忽视f(x)=k两个根都小于零的情况.

练习册系列答案
相关题目
 设函数
设函数