题目内容
 已知函数f(x)=x(1-x2),x∈R.
已知函数f(x)=x(1-x2),x∈R.(1)当x>0时,求f(x)的最大值;
(2)当x>0时,指出f(x)的单调性,并用定义证明;
(3)试作出函数f(x)(x∈R)的简图.
分析:(1)可以利用导数求最大值,也可利用均值不等式进行求解,将f(x)=x(1-x2)变形得y2=x2(1-x2)2=
•2x2(1-x2)(1-x2),利用和定积最大,求出最值,注意等号成立条件.
(2)“f(x)的单调性,并用定义证明”,即设x2>x1>0,比较f(x2)-f(x1)与0的大小.
(3)函数f(x)(x∈R)的简图中必须注明特殊的点:(-1,0)、(0,0)、(1,0),有对称性.
| 1 |
| 2 |
(2)“f(x)的单调性,并用定义证明”,即设x2>x1>0,比较f(x2)-f(x1)与0的大小.
(3)函数f(x)(x∈R)的简图中必须注明特殊的点:(-1,0)、(0,0)、(1,0),有对称性.
解答: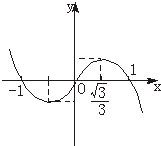 解:(1)∵x>0,欲求f(x)的最大值,必有1-x2>0,
解:(1)∵x>0,欲求f(x)的最大值,必有1-x2>0,
y2=x2(1-x2)2=
•2x2(1-x2)(1-x2)≤
•[
]3=
,
∴y≤
=
.
当且仅当2x2=1-x2,即x=
时,取“=”,即f(x)max=f(
)=
.
(2)由(1)知,
当x∈(0,
]时,f(x)单调递增,x∈[
,+∞)时,f(x)单调递减.
设x2>x1>0,则
f(x2)-f(x1)=-x23+x2-(-x13+x1)
=(x2-x1)-(x2-x1)(x22+x1x2+x12)
=(x2-x1)[1-(x22+x1x2+x12)].
当0<x1<x2≤
时,x2-x1>0,1-(x22+x1x2+x12)>0.
∴f(x2)>f(x1).
∴f(x)在(0,
]上递增.
当
≤x1<x2时,x2-x1>0,1-(x22+x1x2+x12)<0,
∴f(x2)<f(x1).
∴f(x)在[
,+∞)上递减.
(3)注:图象过点(-1,0)、(0,0)、(1,0),关于原点对称.
 解:(1)∵x>0,欲求f(x)的最大值,必有1-x2>0,
解:(1)∵x>0,欲求f(x)的最大值,必有1-x2>0,y2=x2(1-x2)2=
| 1 |
| 2 |
| 1 |
| 2 |
| 2x2+(1-x2)+(1-x2) |
| 3 |
| 4 |
| 27 |
∴y≤
| 2 | ||
3
|
2
| ||
| 9 |
当且仅当2x2=1-x2,即x=
| ||
| 3 |
| ||
| 3 |
2
| ||
| 9 |
(2)由(1)知,
当x∈(0,
| ||
| 3 |
| ||
| 3 |
设x2>x1>0,则
f(x2)-f(x1)=-x23+x2-(-x13+x1)
=(x2-x1)-(x2-x1)(x22+x1x2+x12)
=(x2-x1)[1-(x22+x1x2+x12)].
当0<x1<x2≤
| ||
| 3 |
∴f(x2)>f(x1).
∴f(x)在(0,
| ||
| 3 |
当
| ||
| 3 |
∴f(x2)<f(x1).
∴f(x)在[
| ||
| 3 |
(3)注:图象过点(-1,0)、(0,0)、(1,0),关于原点对称.
点评:本题考查利用基本不等式求最值的方法,函数单调性的证明以及函数图象.
第(1)题也可用导数解决.
∵f′(x)=1-3x2,
令f′(x)=0,∴x=±
.
又x>0,∴x=
.
通过检验单调性知,当x=
时,f(x)取得最大值,其最大值为
,以下解法同上.
第(1)题也可用导数解决.
∵f′(x)=1-3x2,
令f′(x)=0,∴x=±
| ||
| 3 |
又x>0,∴x=
| ||
| 3 |
通过检验单调性知,当x=
| ||
| 3 |
2
| ||
| 9 |

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|