题目内容
【题目】已知某校有歌唱和舞蹈两个兴趣小组，其中歌唱组有 4 名男生，1 名女生，舞蹈组有2 名男生，2 名女生，学校计划从两兴趣小组中各选2名同学参加演出．
（1）求选出的4名同学中至多有2名女生的选派方法数；
（2）记X为选出的4名同学中女生的人数，求X的分布列和数学期望．
【答案】(1)56种 (2)见解析
【解析】
（1）利用间接法求出选出的4名同学中至多有2名女生的选派方法数；（2）由题得X 的可能取值为 0，1，2，3．再求出它们对应的概率，写出分布列，求出数学期望.
解：（1）由题意知，所有的选派方法共有
种，
其中有3名女生的选派方法共有
种，
所以选出的 4 名同学中至多有2名女生的选派方法数为
种．
（2）X 的可能取值为 0，1，2，3．
，
.
，
∴X 的分布列为：
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
∴
天天向上一本好卷系列答案
小学生10分钟应用题系列答案【题目】某校高三文科
名学生参加了
月份的高考模拟考试，学校为了了解高三文科学生的历史、地理学习情况，从名学生中抽取
名学生的成绩进行统计分析，抽出的名学生的地理、历史成绩如下表：
地理 历史 | [80,100] | [60,80） | [40,60） |
[80,100] | 8 | m | 9 |
[60,80） | 9 | n | 9 |
[40,60） | 8 | 15 | 7 |
若历史成绩在[80,100]区间的占30%，
（1）求
的值；
（2）请根据上面抽出的名学生地理、历史成绩，填写下面地理、历史成绩的频数分布表：
[80,100] | [60,80） | [40,60） | |
地理 | |||
历史 |
根据频数分布表中的数据估计历史和地理的平均成绩及方差（同一组数据用该组区间的中点值作代表），并估计哪个学科成绩更稳定.
【题目】下表提供了工厂技术改造后某种型号设备的使用年限x和所支出的维修费y（万元）的几组对照数据:
x（年） | 2 | 3 | 4 | 5 | 6 |
y（万元） | 1 | 2.5 | 3 | 4 | 4.5 |
（1）若知道y对x呈线性相关关系，请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程
；
（2）已知该工厂技术改造前该型号设备使用10年的维修费用为9万元，试根据（1）求出的线性回归方程，预测该型号设备技术改造后，使用10年的维修费用能否比技术改造前降低?参考公式: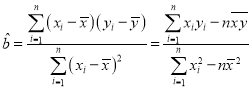
，
.
