题目内容
设M和m分别表示函数y=| 1 | 3 |
分析:利用余弦函数的性质求得cos2x的范围,进而确定函数的值域,则M和m可求,进而求得二者的和.
解答:解:∵0≤cos2x≤1
∴-1≤
cos2x-1≤-
∴M=-
,m=-1
∴M+n=-
故答案为:-
∴-1≤
| 1 |
| 3 |
| 2 |
| 3 |
∴M=-
| 2 |
| 3 |
∴M+n=-
| 5 |
| 3 |
故答案为:-
| 5 |
| 3 |
点评:本题主要考查了三角函数的最值.利用了三角函数的值域.属于基础知识的考查.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
设M和m分别表示函数y=
cosx-1的最大值和最小值,则M+m等于( )
| 1 |
| 3 |
A、
| ||
B、-
| ||
C、-
| ||
| D、-2 |
 cosx-1的最大值和最小值,则M+m等于( )
cosx-1的最大值和最小值,则M+m等于( )
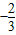

 cos2x-1的最大值和最小值,则M+m等于 .
cos2x-1的最大值和最小值,则M+m等于 .