题目内容
如果函数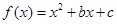 对任意实数
对任意实数 都有
都有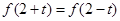 ,那么( )
,那么( )
A. < < < < | B. < < < < |
C. < < < < | D. < < < < |
B
解析试题分析:由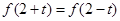 可知,此函数f(x)的对称轴为x=2,由于此二次函数的开口向上,谁离对称轴距离近谁的值小,因为|2-2|<|1-2|<|4-2|,所以
可知,此函数f(x)的对称轴为x=2,由于此二次函数的开口向上,谁离对称轴距离近谁的值小,因为|2-2|<|1-2|<|4-2|,所以 <
< <
< ,故选B.
,故选B.
考点:本小题主要考查了抽象函数对称性的判断方法,以及二次函数的单调性及最值.
点评:一般地说若f(x+a)=f(a-x),那么函数f(x)关于直线x=a对称,据此可知二次函数的对称轴为x=2,结合开口方向和其单调性可确定函数值的大小.

练习册系列答案
相关题目
下列函数中,在(0,2)上为增函数的是( )
A.y=log (x+1) (x+1) | B.y=log2 |
C.y=log2 | D.y=log (x2-4x+5) (x2-4x+5) |
设偶函数f(x)的定义域为R,当x 时f(x)是增函数,则f(-2),f(
时f(x)是增函数,则f(-2),f( ),f(-3)的大小关系是( )
),f(-3)的大小关系是( )
A.f( )>f(-3)>f(-2) )>f(-3)>f(-2) | B.f( )>f(-2)>f(-3) )>f(-2)>f(-3) |
C.f( )<f(-3)<f(-2) )<f(-3)<f(-2) | D.f( )<f(-2)<f(-3) )<f(-2)<f(-3) |
函数
 ,当
,当 时,恒有
时,恒有 ,有( )
,有( )
A.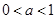 且 且 在 在 上是增函数 上是增函数 |
B.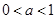 且 且 在 在 上是减函数 上是减函数 |
C. 且 且 在 在 上是增函数 上是增函数 |
D. 且 且 在 在 上是减函数 上是减函数 |
若 ,则【 】
,则【 】
A. | B. | C.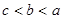 | D. |
当 时,在同一坐标系中,函数
时,在同一坐标系中,函数 的图象是( )
的图象是( )
A. | B. |
C.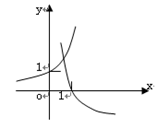 | D. |
若函数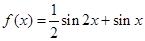 ,则对其导函数
,则对其导函数 值的说法正确的是( )
值的说法正确的是( )
| A.只有最小值 | B.只有最大值 |
| C.既有最大值又有最小值 | D.既无最大值又无最小值 |
 的图象可能是( ).
的图象可能是( ).
 、
、 、
、 、
、 在同一坐标系中的图象如图所示,则
在同一坐标系中的图象如图所示,则 与1的大小关系为 ( )
与1的大小关系为 ( )



