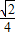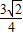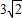题目内容
设a≥0,b≥0,且a2+
=1,则a
的最大值为( )
| b2 |
| 2 |
| 1+b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、3
|
分析:先把a
整理成
•
的形式,把a2+
=1即可求得a2+(
+
)的值,进而根据均值不等式求得答案.
| 1+b2 |
| 2 |
a2(
|
| b2 |
| 2 |
| 1 |
| 2 |
| b 2 |
| 2 |
解答:解:因为a>0,b>0
所以a
=
•
因为a2+(
+
)=a2+
+
=
所以a
≤
×
×
=
故选C
所以a
| 1+b2 |
| 2 |
a2(
|
因为a2+(
| 1 |
| 2 |
| b 2 |
| 2 |
| b2 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
所以a
| 1+b2 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
3
| ||
| 4 |
故选C
点评:本题主要考查了基本不等式在最值问题中的应用.解题的关键是整理出均值不等式的形式.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
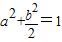 ,则
,则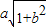 的最大值为( )
的最大值为( )
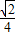
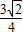
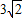
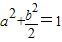 ,则
,则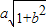 的最大值为( )
的最大值为( )