题目内容
2.在l:x+y-4=0任取一点M,过M且以椭圆$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}$=1的焦点为焦点作椭圆,问M在何处,M到两焦点的距离和最短,并求此椭圆方程.分析 椭圆$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}$=1的焦点分别为F1(-2,0),F2(2,0).设点F2(2,0)关于直线l:x+y-4=0的对称点为P(x,y),利用$\left\{\begin{array}{l}{\frac{x+2}{2}+\frac{y}{2}-4=0}\\{\frac{y}{x-2}=1}\end{array}\right.$,解得P.连接PF1交直线l于点M,求出直线PF1的方程与直线l的方程联立解得M.可以证明点M即为所求.进而得到所求椭圆的方程.
解答  解:椭圆$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}$=1的焦点分别为F1(-2,0),F2(2,0).
解:椭圆$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}$=1的焦点分别为F1(-2,0),F2(2,0).
设点F2(2,0)关于直线l:x+y-4=0的对称点为P(x,y),
则$\left\{\begin{array}{l}{\frac{x+2}{2}+\frac{y}{2}-4=0}\\{\frac{y}{x-2}=1}\end{array}\right.$,解得P(4,2).
连接PF1交直线l于点M,
直线PF1的方程为:x-3y+2=0.
联立$\left\{\begin{array}{l}{x+y-4=0}\\{x-3y+2=0}\end{array}\right.$,解得M$(\frac{5}{2},\frac{3}{2})$.
则M$(\frac{5}{2},\frac{3}{2})$即为所求.
在直线l上除了点M外任取一点Q,则|QF1|+|QP|>|PF1|=|MF1|+|MF2|.
设所求的椭圆标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0).
则2a=|PF1|=$\sqrt{{6}^{2}+{2}^{2}}$=2$\sqrt{10}$,
解得a=$\sqrt{10}$,c=2,b2=a2-c2=6.
∴要求的椭圆标准方程为:$\frac{{x}^{2}}{10}+\frac{{y}^{2}}{6}=1$.
点评 本题考查了椭圆的标准方程及其性质、轴对称问题、中点坐标公式、相互垂直的直线斜率之间的关系,考查了推理能力与计算能力,属于难题.

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
| A. | A⊆B | B. | A与B互斥 | ||
| C. | B⊆A | D. | A与B互为对立事件 |
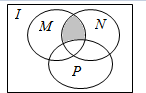 设I是全集,集合M,N,P都是其子集,则图中的阴影部分表示的集合为( )
设I是全集,集合M,N,P都是其子集,则图中的阴影部分表示的集合为( )| A. | M∩(P∩∁IN) | B. | M∩(N∩∁IP) | C. | M∩(∁IN∩∁IM) | D. | (M∩N)∪(M∩P) |