题目内容
在Rt△PAB中,PA=PB,点C、D分别在PA、PB上,且CD∥AB,AB=3,AC=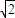 ,则
,则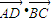 的值为( )
的值为( )A.-7
B.0
C.-3
D.3
【答案】分析:建立直角坐标系,根据条件写出A,B,C,D的坐标,然后求出向量的坐标,代入向量的数量积的坐标表示即可求解
解答: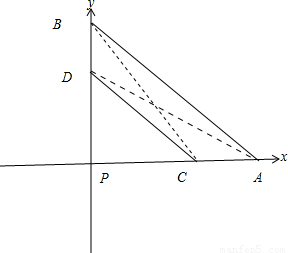 解:建立如图所示的直角坐标系,
解:建立如图所示的直角坐标系,
∵PA=PB,CD∥AB,AB=3,AC=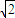
∴PA=PB=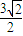 ,PC=
,PC=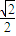
∴A(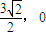 ),B(0,
),B(0,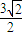 )C(
)C( )D(0,
)D(0,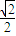 )
)
∴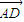 =(-
=(- ),
),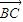 =(
=(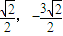 )
)
∴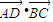 =
=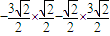 =-3
=-3
故选C
点评:本题主要考查了向量的数量积的求解,解题的关键是建立坐标系,把所求问题坐标化
解答:
 解:建立如图所示的直角坐标系,
解:建立如图所示的直角坐标系,∵PA=PB,CD∥AB,AB=3,AC=
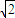
∴PA=PB=
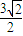 ,PC=
,PC=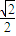
∴A(
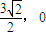 ),B(0,
),B(0,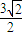 )C(
)C( )D(0,
)D(0,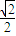 )
)∴
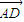 =(-
=(- ),
),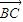 =(
=(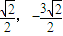 )
)∴
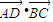 =
=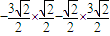 =-3
=-3故选C
点评:本题主要考查了向量的数量积的求解,解题的关键是建立坐标系,把所求问题坐标化

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在Rt△PAB中,∠A是直角,PA=4,AB=3,有一个椭圆以P为一个焦点,另一个焦点Q在AB上,且椭圆经过点A、B.
如图,在Rt△PAB中,∠A是直角,PA=4,AB=3,有一个椭圆以P为一个焦点,另一个焦点Q在AB上,且椭圆经过点A、B.
