题目内容
Rt△ABC中，∠BAC=90°，作AD⊥BC，D为垂足，BD为AB在BC上的射影，CD为AC在BC上的射影，则有AB2+AC2=BC2，AC2=CD·BC成立。直角四面体P-ABC（即PA⊥PB，PB⊥PC，PC⊥PA）中，O为P在△ABC内的射影，△PAB，△PBC，△PCA的面积分别记为S1，S2，S3，△OAB，△OBC，△OCA的面积分别记为S′1，S′2，S′3，△ABC的面积记为S。类比直角三角形中的射影结论，在直角四面体P-ABC中可得到正确结论（ ）（写出一个正确结论即可）。
或
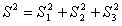（答案不唯一）
练习册系列答案
相关题目
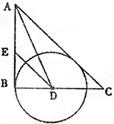16、如图，在Rt△ABC中，∠B=90°，∠A的平分线交BC于D，E为AB上一点，DE=DC，以D为圆心，以DB的长为半径画圆．
（2013•石家庄二模）选修4-1：几何证明选讲
,AB=a,在△ABC内作一系列的正方形，求所有这些正方形的面积和S. 
，点M、N分别在边AB和AC上（点M和点B不重合），将△AMN沿MN翻折到△A′MN，顶点A′恰好落在边BC上（点A′和点B不重合）。
