题目内容
设椭圆 +
+ =1(a>b>0)的左焦点为F1(-2,0),左准线l1与x轴交于点N(-3,0),过点N且倾斜角为30°的直线l交椭圆于A、B两点.
=1(a>b>0)的左焦点为F1(-2,0),左准线l1与x轴交于点N(-3,0),过点N且倾斜角为30°的直线l交椭圆于A、B两点.
(1)求直线l和椭圆的方程;
(2)求证:点F1(-2,0)在以线段AB为直径的圆上.
【答案】
(1)解:可知直线l:y= (x+3).
(x+3).
由c=2及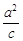 =3,解得a2=6,
=3,解得a2=6,
∴b2=6-22=2.∴椭圆方程为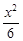 +
+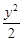 =1.
=1.
 (2)证明:联立方程组
(2)证明:联立方程组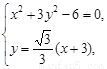
将②代入①,整理得2x2+6x+3=0.
设A(x1,y1)、B(x2,y2),则x1+x2=-3,x1x2=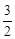 .
.
方法一:k ·k
·k =
=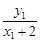 ·
·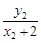 =
=
=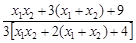 =
=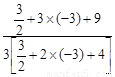 =-1,
=-1,
∴F1A⊥F1B,即∠AF1B=90°.
∴点F1(-2,0)在以线段AB为直径的圆上.
方法二: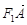 ·
·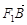 =(x1+2,y1)·(x2+2,y2)=(x1+2)(x2+2)+y1y2
=(x1+2,y1)·(x2+2,y2)=(x1+2)(x2+2)+y1y2
=x1x2+2(x1+x2)+4+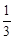 [x1x2+3(x1+x2)+9]
[x1x2+3(x1+x2)+9]
=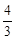 x1x2+3(x1+x2)+7=0,
x1x2+3(x1+x2)+7=0,
∴F1A⊥F1B,则∠AF1B=90°.
∴点F1(-2,0)在以线段AB为直径的圆上.
【解析】略

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目