题目内容

设椭圆+=1(a>b>0)的左焦点为F,离心率为,过点F且与x轴垂直的直线被椭圆截得的线段长为.

(1)求椭圆的方程;

(2)设A,B分别为椭圆的左、右顶点,过点F且斜率为k的直线与椭圆交于C,D两点.若·+·=8,求k的值.

 

【答案】

(1) 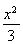+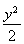=1 (2) k=±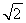

【解析】

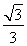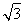解:(1)设F(-c,0),由=,知a=c.

过点F且与x轴垂直的直线为x=-c,

代入椭圆方程有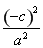+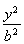=1,

解得y=±,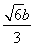

于是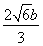=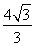,解得b=,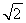

又a2-c2=b2,从而a=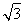,c=1,

所以椭圆的方程为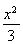+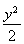=1.

(2)设点C(x1,y1),D(x2,y2),

由F(-1,0)得直线CD的方程为y=k(x+1).

由方程组消去y,整理得(2+3k2)x2+6k2x+3k2-6=0,

则x1+x2=-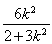,x1x2=.

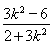因为A(-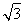,0),B(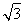,0),

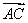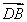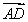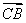所以·+·=(x1+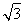,y1)·(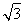-x2,-y2)+(x2+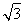,y2)·(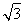-x1,-y1)=6-2x1x2-2y1y2=6-2x1x2-2k2(x1+1)(x2+1)

=6-(2+2k2)x1x2-2k2(x1+x2)-2k2=6+.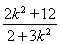

由已知得6+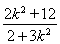=8,解得k=±.

 

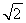练习册系列答案
相关题目
已知椭圆E：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
3
2
，其长轴长与短轴长的和等于6．
（1）求椭圆E的方程；
（2）如图，设椭圆E的上、下顶点分别为A1、A2，P是椭圆上异于A1、A2的任意一点，直线PA1、PA2分别交x轴于点N、M，若直线OT与过点M、N的圆G相切，切点为T．证明：线段OT的长为定值．
（2012•佛山二模）已知椭圆E：
x2
a2
+
y2
b2
=1(a＞b＞0)的一个交点为F1(-
3
，0)，而且过点H(
3
，
1
2
)．
（Ⅰ）求椭圆E的方程；
（Ⅱ）设椭圆E的上下顶点分别为A1，A2，P是椭圆上异于A1，A2的任一点，直线PA1，PA2分别交x轴于点N，M，若直线OT与过点M，N的圆G相切，切点为T．证明：线段OT的长为定值，并求出该定值．
已知椭圆G：
x2
a2
+
y2
b2
=1(a＞b＞0)的离心率为e=
2
3
，椭圆G上的点N到两焦点的距离之和为12，点A、B分别是椭圆G长轴的左、右端点，点F是椭圆的右焦点．点P在椭圆上，且位于x轴的上方，PA⊥PF．
（1）求椭圆G的方程；
（2）求点P的坐标；
（3）设M是椭圆长轴AB上的一点，M到直线AP的距离等于|MB|，求椭圆上的点到点M的距离d的最小值．
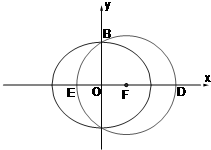精英家教网如图，已知F（c，0）是椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的右焦点；⊙F：（x-c）2+y2=a2与x轴交于D，E两点，其中E是椭圆C的左焦点．
（1）求椭圆C的离心率；
（2）设⊙F与y轴的正半轴的交点为B，点A是点D关于y轴的对称点，试判断直线AB与⊙F的位置关系；
（3）设直线BF与⊙F交于另一点G，若△BGD的面积为4
3
，求椭圆C的标准方程．
设椭圆=1(a＞b＞0)的焦点分别为F1(-1,0)、F2(1,0),右准线l交x轴于点A,且.

(1)试求椭圆的方程;

(2)过F1、F2分别作互相垂直的两直线与椭圆分别交于D、E、M、N四点(如图所示),试求四边形DMEN面积的最大值和最小值.

(文)已知函数f(x)=x3+bx2+cx,b、c∈R,且函数f(x)在区间(-1,1)上单调递增,在区间(1,3)上单调递减.

(1)若b=-2,求c的值;

(2)求证:c≥3;

(3)设函数g(x)=f′(x),当x∈［-1,3］时,g(x)的最小值是-1,求b、c的值.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网