题目内容
设椭圆 +
+ =1(a>b>0)的左,右焦点分别为F1,F2,点P(a,b)满足|PF2|=|F1F2|.
=1(a>b>0)的左,右焦点分别为F1,F2,点P(a,b)满足|PF2|=|F1F2|.
(1)求椭圆的离心率e;
(2)设直线PF2与椭圆相交于A,B两点.若直线PF2与圆(x+1)2+(y- )2=16相交于M,N两点,且|MN|=
)2=16相交于M,N两点,且|MN|= |AB|,求椭圆的方程.
|AB|,求椭圆的方程.
【答案】
(1) 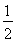 (2)
(2) 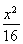 +
+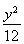 =1
=1
【解析】
解:(1)设F1(-c,0),F2(c,0)(c>0),
因为|PF2|=|F1F2|,
所以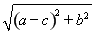 =2c,
=2c,
整理得2(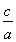 )2+
)2+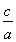 -1=0,
-1=0,
得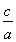 =-1(舍去),或
=-1(舍去),或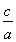 =
=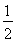 ,
,
所以e=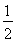 .
.
(2)由(1)知a=2c,b=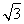 c,
c,
可得椭圆方程为3x2+4y2=12c2,
直线PF2的方程为y=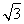 (x-c).
(x-c).
A、B两点的坐标满足方程组
消去y并整理,得5x2-8cx=0,
解得x1=0,x2=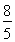 c.
c.
得方程组的解

不妨设A(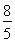 c,
c, c),B(0,-
c),B(0,-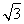 c),
c),
所以|AB|=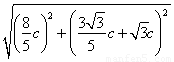 =
=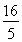 c.
c.
于是|MN|=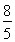 |AB|=2c.
|AB|=2c.
圆心(-1,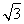 )到直线PF2的距离
)到直线PF2的距离
d= =
=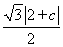 .
.
因为d2+ =42,
=42,
所以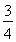 (2+c)2+c2=16.
(2+c)2+c2=16.
整理得7c2+12c-52=0,
解得c=-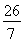 (舍去)或c=2.
(舍去)或c=2.
所以椭圆方程为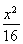 +
+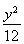 =1.
=1.

练习册系列答案
相关题目
 已知椭圆E:
已知椭圆E: (2012•佛山二模)已知椭圆E:
(2012•佛山二模)已知椭圆E: 如图,已知F(c,0)是椭圆
如图,已知F(c,0)是椭圆