题目内容
 如图,平面α,β,γ两两互相垂直,长为
如图,平面α,β,γ两两互相垂直,长为| 7 |
| 6 |
分析:利用题中条件:“平面α、β、γ两两互相垂直”建立一个长方体,将AB放置在此长方体中解决,再根据长方体对角线长定理用a,b,c表示出对角线AC1的长,最后求出它的取值范围即可.
解答:解:构造长方体如图,该长方体的对角线长
,
三个面上的对角线长分别为:
、a、b,
则
(a2+b2+6)=7,
∴a2+b2=8,
∵a+b≤
=
=4,
则a+b的最大值为4.
故选A.
| 7 |

三个面上的对角线长分别为:
| 6 |
则
| 1 |
| 2 |
∴a2+b2=8,
∵a+b≤
| 2(a2+b2) |
| 2×8 |
则a+b的最大值为4.
故选A.
点评:本题主要考查了棱柱的结构特征、点、线、面间的距离计算,考查空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
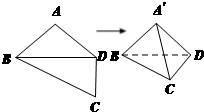 如图,平面四边形ABCD中,AB=AD=CD=1,BD=
如图,平面四边形ABCD中,AB=AD=CD=1,BD=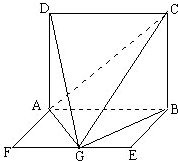 如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,G是线段EF的中点,且B点在平面AGC内的射影在CG上.
如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,G是线段EF的中点,且B点在平面AGC内的射影在CG上. 如图,平面PAD⊥平面ABCD,四边形ABCD为正方形,△PAD是直角三角形,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.
如图,平面PAD⊥平面ABCD,四边形ABCD为正方形,△PAD是直角三角形,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点. 如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,
如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA, 如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,BD=
如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,BD=