题目内容
 如图,平面PAD⊥平面ABCD,四边形ABCD为正方形,△PAD是直角三角形,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.
如图,平面PAD⊥平面ABCD,四边形ABCD为正方形,△PAD是直角三角形,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.(1)求证:EF⊥平面PAB;
(2)求异面直线EG与BD所成的角的余弦值.
分析:解法一:(1)由题意可证明AD⊥面PAB,E、F分别是线段PA、PD的中点,EF∥AD,从而得证;
(2)取BC的中点M,取DC的中点G,连接GM、AM、EM,则GM∥BD,∠EGM(或其补角)就是异面直线EG与BD所成的角.
分别求得EM、EG、MG的长度,再利用余弦定理即可求得异面直线EG与BD所成的角的余弦值.
解法二:(1)建立如图所示的空间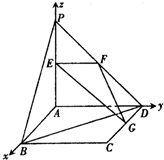 直角坐标系A-xyz,
直角坐标系A-xyz,
A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),
P(0,0,2),E(0,0,1),F(0,1,1),G(1,2,0).
求得
=(0,1,0),
=(0,0,2),
=(2,0,0),
利用
•
=0,
•
=0,可证得EF⊥AP,EF⊥AB,从而可证平面EFG⊥平面PAB.
(2)求得
=(1,2,-1),
=(-2,2,0),利用向量的夹角公式可求得异面直线EG与BD所成的角的余弦值为
.
(2)取BC的中点M,取DC的中点G,连接GM、AM、EM,则GM∥BD,∠EGM(或其补角)就是异面直线EG与BD所成的角.
分别求得EM、EG、MG的长度,再利用余弦定理即可求得异面直线EG与BD所成的角的余弦值.
解法二:(1)建立如图所示的空间
 直角坐标系A-xyz,
直角坐标系A-xyz,A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),
P(0,0,2),E(0,0,1),F(0,1,1),G(1,2,0).
求得
| EF |
| AP |
| AB |
利用
| EF |
| AP |
| EF |
| AB |
(2)求得
| EG |
| BD |
| ||
| 6 |
解答: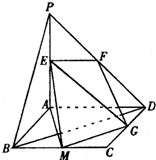 解法一:(1)证明:∵ABCD为正方形,△PAD是直角三角形,且PA=AD=2,
解法一:(1)证明:∵ABCD为正方形,△PAD是直角三角形,且PA=AD=2,
∴AD⊥AB,AD⊥PA,又AB∩PA=A,(2分)
∴AD⊥面PAB.
∵E、F分别是线段PA、PD的中点,
∴EF∥AD,
∴EF⊥面PAB.(6分)
(2)解:取BC的中点M,取DC的中点G,连接GM、AM、EM,则GM∥BD,(8分)
∴∠EGM(或其补角)就是异面直线EG与BD所成的角.(10分)
在Rt△MAE中,EM=
=
,同理EG=
,
又GM=
BD=
,
∴在△MGE中,cos∠EGM=
=
=
…
故异面直线EG与BD所成的角的余弦值为
.(14分)
解法二:建立如图所示的空间 直角坐标系A-xyz,
直角坐标系A-xyz,
则A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),
P(0,0,2),E(0,0,1),F(0,1,1),G(1,2,0).
(1)证明:∵
=(0,1,0),
=(0,0,2),
=(2,0,0),
∴
•
=0×0+1×0+0×2=0,
•
=0×2+1×0+0×0=0,
∴EF⊥AP,EF⊥AB.
又∵AP、AB?面PAB,且PA∩AB=A,
∴EF⊥平面PAB.又EF?面EFG,
∴平面EFG⊥平面PAB.
(2)解:∵
=(1,2,-1),
=(-2,2,0),
∴cos<
,
>=
=
=
,
故异面直线EG与BD所成的角的余弦值为
.
 解法一:(1)证明:∵ABCD为正方形,△PAD是直角三角形,且PA=AD=2,
解法一:(1)证明:∵ABCD为正方形,△PAD是直角三角形,且PA=AD=2,∴AD⊥AB,AD⊥PA,又AB∩PA=A,(2分)
∴AD⊥面PAB.
∵E、F分别是线段PA、PD的中点,
∴EF∥AD,
∴EF⊥面PAB.(6分)
(2)解:取BC的中点M,取DC的中点G,连接GM、AM、EM,则GM∥BD,(8分)
∴∠EGM(或其补角)就是异面直线EG与BD所成的角.(10分)
在Rt△MAE中,EM=
| EA2+AM2 |
| 6 |
| 6 |
又GM=
| 1 |
| 2 |
| 2 |
∴在△MGE中,cos∠EGM=
| EG2+GM2-ME2 |
| 2EG•GM |
| 6+2-6 | ||||
2
|
| ||
| 6 |
故异面直线EG与BD所成的角的余弦值为
| ||
| 6 |
解法二:建立如图所示的空间
 直角坐标系A-xyz,
直角坐标系A-xyz,则A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),
P(0,0,2),E(0,0,1),F(0,1,1),G(1,2,0).
(1)证明:∵
| EF |
| AP |
| AB |
∴
| EF |
| AP |
| EF |
| AB |
∴EF⊥AP,EF⊥AB.
又∵AP、AB?面PAB,且PA∩AB=A,
∴EF⊥平面PAB.又EF?面EFG,
∴平面EFG⊥平面PAB.
(2)解:∵
| EG |
| BD |
∴cos<
| EG |
| BD |
| ||||
|
|
| -2+4 | ||||
|
| ||
| 6 |
故异面直线EG与BD所成的角的余弦值为
| ||
| 6 |
点评:本题考查直线与平面垂直的判定与异面直线及其所成的角,着重考查直线与平面垂直的判定定理的应用及余弦定理解三角形的应用,突出考查几何法与坐标法,属于难题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 18、如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.
18、如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.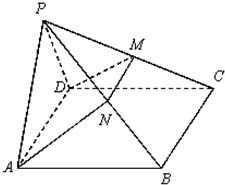 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.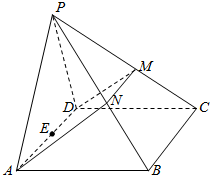 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点.
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点.