题目内容
已知数列 是首项为
是首项为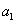 ,公比为
,公比为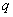 的等比数列.
的等比数列.
(1)求和:①
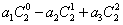 ;
;
②  ;
;
③ 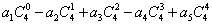 ;
;
(2)根据(1)求得的结果,试归纳出关于正整数 的一个结论(不需证明);
的一个结论(不需证明);
(3)设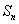 是等比数列
是等比数列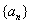 的前
的前 项和,求:
项和,求:
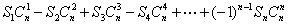 .
.
【答案】
(1)∵ 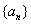 成等比数列, ∴
成等比数列, ∴
 ,
,
∴ ① 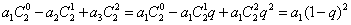 ; ……2分
; ……2分
② 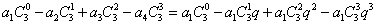
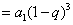 ;
………………3分
;
………………3分
③ 
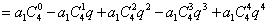
 .
………………4分
.
………………4分
(2)由(1)可归纳得
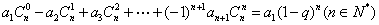 . …………6分
. …………6分
(3)① 当 时,
时, ,则
,则
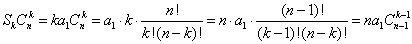 ,…8分
,…8分
∴ 
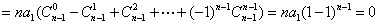 ;……………11分
;……………11分
② 当 时,
时,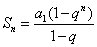 ,则
,则
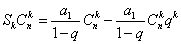 , ………………13分
, ………………13分
∴ 

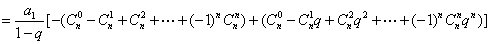
 .
………………16分
.
………………16分

练习册系列答案
相关题目
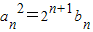 .若不等式
.若不等式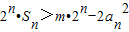 对?n∈N*恒成立,求m的取值范围.
对?n∈N*恒成立,求m的取值范围.