题目内容
如果一个数列的各项都是实数,且从第二项起,每一项与它的前一项的平方差是同一个常数,则称该数列为等方差数列,这个常数叫这个数列的公方差.(Ⅰ)若数列{an}既是等方差数列,又是等差数列,求证:该数列是常数列;
(Ⅱ)已知数列{an}是首项为2,公方差为2的等方差数列,数列{bn}的前n项和为Sn,且满足
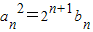 .若不等式
.若不等式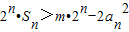 对?n∈N*恒成立,求m的取值范围.
对?n∈N*恒成立,求m的取值范围.
【答案】分析:(Ⅰ)依题 ,通过分解因式,利用{an}为等差数列,设公差为d,求出d=0,说明{an}是常数列.
,通过分解因式,利用{an}为等差数列,设公差为d,求出d=0,说明{an}是常数列.
(Ⅱ)通过 为首项为4,公差为2的等差数列,求出
为首项为4,公差为2的等差数列,求出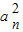 ,由
,由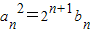 得bn,利用错位相减法求出Sn,通过不等式
得bn,利用错位相减法求出Sn,通过不等式 ,推出
,推出 恒成立,由归纳法原理推出n≥4时,3k+1<2k,求出m的取值范围为m≤3.
恒成立,由归纳法原理推出n≥4时,3k+1<2k,求出m的取值范围为m≤3.
解答:解:(Ⅰ)依题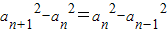
⇒(an+1-an)(an+1+an)=(an-an-1)(an+an-1)
又{an}为等差数列,设公差为d,
则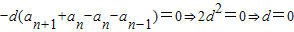
故{an}是常数列.(4分)
(Ⅱ)由{an}是首项为2,公方差为2的等方差数列.
即 为首项为4,公差为2的等差数列,
为首项为4,公差为2的等差数列, (6分)
(6分)
由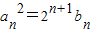 得
得
 ①
①
 ②
②
 (10分)
(10分)
不等式 即3•2n-(n+3)>m•2n-4n-4也即(m-3)•2n<3n+1,即
即3•2n-(n+3)>m•2n-4n-4也即(m-3)•2n<3n+1,即 恒成立
恒成立
由于n=1,2,3时,3n+1>2n;n=4时,3n+1<2n;
假设n=k(k≥4)时,3k+1<2k,
那么2k+1=2•2k>2(3k+1)=3(k+1)+1+(3k-2)>3(k+1)+1,
由归纳法原理知:n≥4时,3k+1<2k,
所以 ⇒m-3≤0,
⇒m-3≤0,
故m的取值范围为m≤3(14分)
点评:本题考查新定义的应用,数列特征的判断,数列求和的错位相减法的应用,转化思想,计算能力.
 ,通过分解因式,利用{an}为等差数列,设公差为d,求出d=0,说明{an}是常数列.
,通过分解因式,利用{an}为等差数列,设公差为d,求出d=0,说明{an}是常数列.(Ⅱ)通过
 为首项为4,公差为2的等差数列,求出
为首项为4,公差为2的等差数列,求出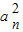 ,由
,由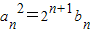 得bn,利用错位相减法求出Sn,通过不等式
得bn,利用错位相减法求出Sn,通过不等式 ,推出
,推出 恒成立,由归纳法原理推出n≥4时,3k+1<2k,求出m的取值范围为m≤3.
恒成立,由归纳法原理推出n≥4时,3k+1<2k,求出m的取值范围为m≤3.解答:解:(Ⅰ)依题
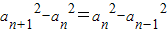
⇒(an+1-an)(an+1+an)=(an-an-1)(an+an-1)
又{an}为等差数列,设公差为d,
则
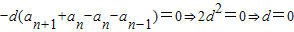
故{an}是常数列.(4分)
(Ⅱ)由{an}是首项为2,公方差为2的等方差数列.
即
 为首项为4,公差为2的等差数列,
为首项为4,公差为2的等差数列, (6分)
(6分)由
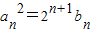 得
得
 ①
① ②
②
 (10分)
(10分)不等式
 即3•2n-(n+3)>m•2n-4n-4也即(m-3)•2n<3n+1,即
即3•2n-(n+3)>m•2n-4n-4也即(m-3)•2n<3n+1,即 恒成立
恒成立由于n=1,2,3时,3n+1>2n;n=4时,3n+1<2n;
假设n=k(k≥4)时,3k+1<2k,
那么2k+1=2•2k>2(3k+1)=3(k+1)+1+(3k-2)>3(k+1)+1,
由归纳法原理知:n≥4时,3k+1<2k,
所以
 ⇒m-3≤0,
⇒m-3≤0,故m的取值范围为m≤3(14分)
点评:本题考查新定义的应用,数列特征的判断,数列求和的错位相减法的应用,转化思想,计算能力.

练习册系列答案
相关题目
 是首项为2,公方差为2的等方差数列,若将
是首项为2,公方差为2的等方差数列,若将 这种顺序的排列作为某种密码,则这种密码的个数为
这种顺序的排列作为某种密码,则这种密码的个数为