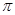题目内容
关于函数 ,下列命题:
,下列命题:①若存在x1,x2有x1-x2=π时,f(x1)=f(x2)成立;
②f(x)在区间
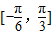 上是单调递增;
上是单调递增; ③函数f(x)的图象关于点
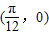 成中心对称图象;
成中心对称图象; ④将函数f(x)的图象向左平移
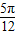 个单位后将与y=2sin2x的图象重合.
个单位后将与y=2sin2x的图象重合.其中正确的命题序号 (注:把你认为正确的序号都填上)
【答案】分析:根据二倍角公式,可化简函数的解析式为正弦型函数的形式,根据函数的周期性可判断①;根据函数的单调性可判断②;根据函数的对称性可判断③;根据函数图象的变换法则可判断④.
解答:解:函数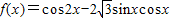 =
=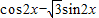 =2sin(2x+
=2sin(2x+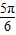 )
)
由ω=2,故函数的周期为π,故x1-x2=π时,f(x1)=f(x2)成立,故①正确;
由2x+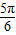 ∈[-
∈[-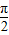 +2kπ,
+2kπ,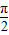 +2kπ]得,x∈[-
+2kπ]得,x∈[-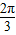 +kπ,-
+kπ,-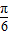 +2kπ](k∈Z),故[-
+2kπ](k∈Z),故[-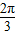 ,-
,-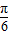 ]是函数的单调增区间,区间
]是函数的单调增区间,区间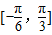 应为函数的单调减区间,故②错误;
应为函数的单调减区间,故②错误;
当x=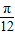 时,f(x)=0,故点
时,f(x)=0,故点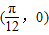 是函数图象的对称中心,故③正确;
是函数图象的对称中心,故③正确;
函数f(x)的图象向左平移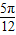 个单位后得到函数的解析式为f(x)=2sin[2(x+
个单位后得到函数的解析式为f(x)=2sin[2(x+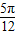 )+
)+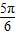 ]=2sin(2x+
]=2sin(2x+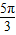 ),故④错误
),故④错误
故答案为:①③
点评:本题以命题的真假判断为载体考查了三角函数的图象和性质,熟练掌握三角函数的图象和性质是解答的关键.
解答:解:函数
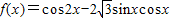 =
=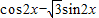 =2sin(2x+
=2sin(2x+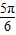 )
)由ω=2,故函数的周期为π,故x1-x2=π时,f(x1)=f(x2)成立,故①正确;
由2x+
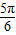 ∈[-
∈[-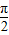 +2kπ,
+2kπ,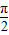 +2kπ]得,x∈[-
+2kπ]得,x∈[-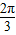 +kπ,-
+kπ,-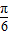 +2kπ](k∈Z),故[-
+2kπ](k∈Z),故[-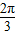 ,-
,-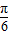 ]是函数的单调增区间,区间
]是函数的单调增区间,区间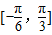 应为函数的单调减区间,故②错误;
应为函数的单调减区间,故②错误;当x=
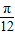 时,f(x)=0,故点
时,f(x)=0,故点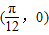 是函数图象的对称中心,故③正确;
是函数图象的对称中心,故③正确;函数f(x)的图象向左平移
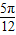 个单位后得到函数的解析式为f(x)=2sin[2(x+
个单位后得到函数的解析式为f(x)=2sin[2(x+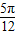 )+
)+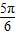 ]=2sin(2x+
]=2sin(2x+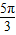 ),故④错误
),故④错误故答案为:①③
点评:本题以命题的真假判断为载体考查了三角函数的图象和性质,熟练掌握三角函数的图象和性质是解答的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
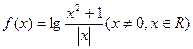 有下列命题:
有下列命题: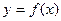 的图象关于y轴对称 ②在
的图象关于y轴对称 ②在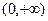 上
上 是增函数;在
是增函数;在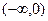 上
上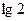 ④在
④在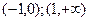 上
上 有下列命题:
有下列命题: 是以
是以 为最小正周期的周期函数;
为最小正周期的周期函数; ;
; 对称;
对称; 对称;其中正确的序号为 。
对称;其中正确的序号为 。 有下列命题:
有下列命题: 是以
是以 为最小正周期的周期函数;
为最小正周期的周期函数; ;
; 对称;
对称; 对称;其中正确的序号为 。
对称;其中正确的序号为 。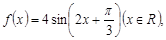 有下列命题:
有下列命题: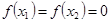 可得
可得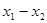 必是π的整数倍;
必是π的整数倍;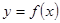 的表达式可改写为
的表达式可改写为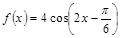 ;
;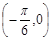 对称;
对称;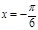 对称.以上命题成立的序号是__________________.
对称.以上命题成立的序号是__________________.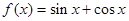 ,下列命题正确的是 ( )
,下列命题正确的是 ( )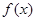 最大值为2
最大值为2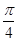 个单位后对应的函数是奇函数
个单位后对应的函数是奇函数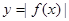 的周期为2
的周期为2