题目内容
(10分)为了了解某学校餐厅的饭菜质量问题,采用分层抽样的方法从高一、高二、高三三个年级中抽取6个班进行调查,已知高一、高二、高三年级分别有18、12、6个班.
①求从高一、高二、高三年级分别抽取的班级个数;
②若从抽取的6个班中随机抽取2个进行调查结果的对比,试列出所有可能的抽取结果,并且计算抽取的2个班中至少有1个来自高一年级的概率.
①从高一、高二、高三年级分别抽取的班级个数3,2,1;②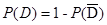 =1-
=1-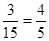
解析试题分析:(1)由题意知总体个数是6+8+12,要抽取的个数是6,做出每个个体被抽到的概率,分别用三个年级的数目乘以概率,得到每一个年级要抽取的班数.
(2)由题意知本题是一个古典概型,从6个班中随机地抽取2个班共有C62个等可能的结果,其中这两个班都来自高二、三年级的共有C32个结果,这两个班来自至少有一个来自高一年级的共有C62- C32个结果,得到概率.
解:①从高一、高二、高三年级分别抽取的班级个数3,2,1;
②抽取的6个班中,高一三个班记为: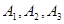 ;高二两个班记为:
;高二两个班记为: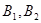 ;高三一个班记为:
;高三一个班记为: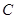 ,则抽取2个班的所有可能结果为:
,则抽取2个班的所有可能结果为: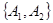 ,
,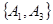 ,
,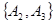 ,
,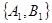 ,
,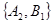 ,
,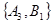 ,
,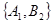 ,
,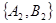 ,
,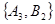 ,
,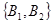 ,
,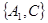 ,
,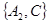 ,
,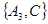 ,
,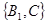 ,
,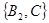 , 共15种.
, 共15种.
抽取的2个班中至少有1个来自高一年级,记为事件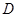 ,则事件
,则事件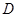 的对立事件
的对立事件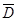 包括:
包括: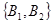 ,
,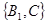 ,
,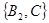 ,共3种,故
,共3种,故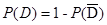 =1-
=1-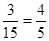
考点:本题考查分层抽样,考查古典概型的概率公式,是一个基础题,可以作为解答题目出现在大型考试中,是一个送分题目
点评:解决该试题的关键是理解分层抽样的等比例性质,以及古典概型概率中试验的总体数和事件发生个基本事件数。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
某校为了解学生的学科学习兴趣,对初高中学生做了一个喜欢数学和喜欢语文的抽样调查,随机抽取了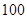 名学生,相关的数据如下表所示:
名学生,相关的数据如下表所示:
| | 数学 | 语文 | 总计 |
| 初中 | 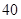 | 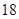 | 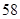 |
| 高中 | 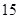 | 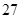 | 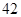 |
| 总计 | 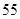 | 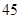 | 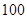 |
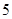 名,高中学生应该抽取几名?
名,高中学生应该抽取几名?(2) 在(1)中抽取的
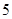 名学生中任取
名学生中任取 名,求恰有
名,求恰有 名初中学生的概率.
名初中学生的概率. (本小题满分12分)某种产品的广告费支出 与销售额
与销售额 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据:
 | 2 | 4 | 5 | 6 | 8 |
 | 30 | 40 | 60 | 50 | 70 |
(2)请根据上表提供的数据,用最小二乘法求出
 关于
关于 的线性回归方程
的线性回归方程 .(其中
.(其中 )
) 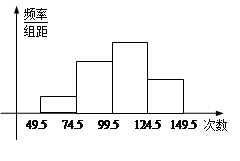
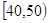 ,
,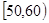 …
… 后画出如下频率分布直方图,根据图形中所给的信息,回答以下问题:
后画出如下频率分布直方图,根据图形中所给的信息,回答以下问题: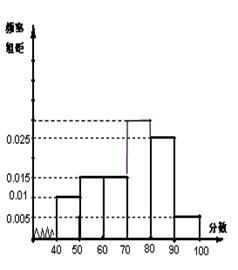
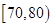 的频率.
的频率.
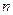 件,合格率为96%,在投放市场之前,决定对该产品进行最后检验,为了减少检验次数,科技人员采用打包的形式进行,即把
件,合格率为96%,在投放市场之前,决定对该产品进行最后检验,为了减少检验次数,科技人员采用打包的形式进行,即把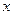 件打成一包,对这
件打成一包,对这 果检测仪器显示绿灯,说明该包产品均为合格品;如果检测仪器显示红灯,说明该包产品至少有一件不合格,须对该包产品一共检测了
果检测仪器显示绿灯,说明该包产品均为合格品;如果检测仪器显示红灯,说明该包产品至少有一件不合格,须对该包产品一共检测了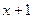 次
次 测这
测这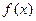 ;
;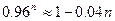 ,要使检测次数最少,则每包应放多少件产品?
,要使检测次数最少,则每包应放多少件产品?