题目内容
【题目】某乳业公司生产甲、乙两种产品,需要A,B,C三种苜蓿草饲料,生产1个单位甲种产品和生产1个单位乙种产品所需三种苜蓿草饲料的吨数如下表所示:
产品 苜蓿草饲料 | A | B | C |
甲 | 4 | 8 | 3 |
乙 | 5 | 5 | 10 |
现有A种饲料200吨,B种饲料360吨,C种饲料300吨,在此基础上生产甲乙两种产品,已知生产1个单位甲产品,产生的利润为2万元;生产1个单位乙产品,产生的利润为3万元,分别用x,y表示生产甲、乙两种产品的数量.
(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问分别生产甲乙两种产品多少时,能够产出最大的利润?并求出此最大利润.
【答案】(1)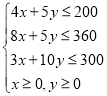 ;图见解析;(2)当甲产品生产
;图见解析;(2)当甲产品生产![]() 吨,乙产品生产
吨,乙产品生产![]() 吨时,利润最大,最大利润为
吨时,利润最大,最大利润为![]() 万元
万元
【解析】
(1)根据三种饲料的数量和生产每吨甲乙产品的消耗量可构造不等式,由此可得满足条件的不等式组即为所求数学关系式;由线性规划知识可画出对应的平面区域;
(2)设利润![]() ,将问题转化为
,将问题转化为![]() 在
在![]() 轴截距最大问题的求解,通过直线平移可确定最大值点,代入可求得结果.
轴截距最大问题的求解,通过直线平移可确定最大值点,代入可求得结果.
(1)![]() 种饲料有
种饲料有![]() 吨,则
吨,则![]() ;
;![]() 种饲料有
种饲料有![]() 吨,则
吨,则![]() ;
;
![]() 种饲料有
种饲料有![]() 吨,则
吨,则![]() ,又
,又![]() ,
,![]()
![]() 满足生产条件的数学关系式为
满足生产条件的数学关系式为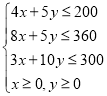
所对应的平面区域如下图阴影部分所示:
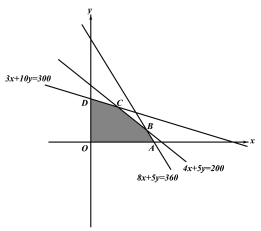
(2)设利润为![]() ,则
,则![]()
当![]() 取最大值时,
取最大值时,![]() 在
在![]() 轴截距最大
轴截距最大
由![]() 平移可知,当
平移可知,当![]() 过点
过点![]() 时,在
时,在![]() 轴截距最大
轴截距最大
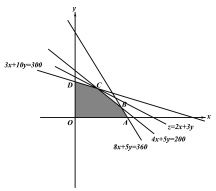
由![]() 得:
得:![]()
![]()
![]() 当甲产品生产
当甲产品生产![]() 吨,乙产品生产
吨,乙产品生产![]() 吨时,利润最大,最大利润为
吨时,利润最大,最大利润为![]() 万元
万元

练习册系列答案
相关题目