题目内容
12．在△ABC中，角A，B，C的对边分别是a，b，c，且A=2B，则$\frac{sinB}{sin3B}$等于（ ）| A． | $\frac{a}{c}$ | B． | $\frac{c}{b}$ | C． | $\frac{b}{a}$ | D． | $\frac{b}{c}$ |
分析 由已知及三角形内角和定理，诱导公式可得$\frac{sinB}{sin3B}$=$\frac{sinB}{sin（A+B）}$=$\frac{sinB}{sin（π-C）}$=$\frac{sinB}{sinC}$，再结合正弦定理即可得解．
解答 解：∵A+B+C=π，A=2B，
∴$\frac{sinB}{sin3B}$=$\frac{sinB}{sin（A+B）}$=$\frac{sinB}{sin（π-C）}$=$\frac{sinB}{sinC}$．
再结合正弦定理得：$\frac{sinB}{sinC}=\frac{b}{c}$．
故选：D．
点评 本题主要考查了三角形内角和定理，诱导公式，正弦定理的应用，熟练掌握相关定理是解题的关键，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
20．若A={x|x＜1}，B={x|x2+2x＞0}，则A∩B=（ ）
| A． | （0，1） | B． | （-∞，-2） | C． | （-2，0） | D． | （-∞，-2）∪（0，1） |
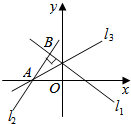如果直线l1的倾斜角是150°，l2⊥l1，垂足为B，l1，l2与x轴分别相交于点C，A，l3平分∠BAC，则l3的倾斜角为30°．
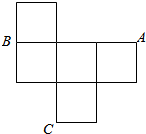如图是一个无盖的正方体盒子展开后的平面图，A，B，C展开图是上的三点，则在正方体盒子中，∠ABC=90°．