题目内容
定义在R上的偶函数f(x)的一个单调递增区间为(3,5),则y=f(x-1)
| A.图象的对称轴为x=-1,且在(2,4)内递增 |
| B.图象的对称轴为x=-1,且在(2,4)内递减 |
| C.图象的对称轴为x=1,且在(4,6)内递增 |
| D.图象的对称轴为x=1,且在(4,6)内递减 |
C
解析试题分析:因为定义在R上的偶函数f(x)的一个单调递增区间为(3,5),所以可知在区间(-5,-3)是递减的去甲,同时那么对于y=f(x-1)是将原函数向右平移一个单位,因此单调增区间为(4,6),那么对称轴为x=1,故排除选项A,B,那么同时结合单调性可知排除D,故选C.
考点:本试题考查了函数的对称性和单调性的运用。
点评:解决该试题的关键是对于图像变换的准确的理解,以及平移变换对于函数图像和性质的影响,属于基础题。

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
若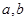 是任意实数,且
是任意实数,且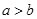 ,则( )
,则( )
A.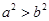 | B. | C.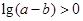 | D.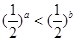 |
已知 且
且 ,则
,则
| A.有最大值2 | B.有最大值4 | C.有最小值3 | D.等于4 |
已知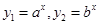 是指数函数,
是指数函数,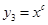 ,
, 是幂函数,它们的图象如右图所示,则
是幂函数,它们的图象如右图所示,则 的大小关系为
的大小关系为 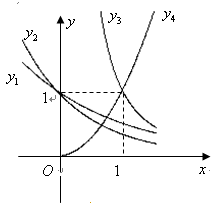
A. | B.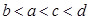 |
C.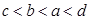 | D.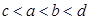 |
下列所给4个图象中,与所给3件事吻合最好的顺序为( )
(1)我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;
(2)我骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
(3)我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速。
| A.(1)(2)(4) | B.(4)(2)(3) |
| C.(4)(1)(3) | D.(4)(1)(2) |
函数 的定义域为( )
的定义域为( )
A. | B.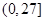 | C. | D. |
对实数 和
和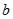 ,定义运算“
,定义运算“ ”:
”: 设函数
设函数 ,
, ,若函数
,若函数 的图像与
的图像与 轴恰有两个公共点,则实数
轴恰有两个公共点,则实数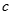 的取值范围是( )
的取值范围是( )
A.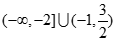 | B. |
C. | D. |
函数 的零点所在的大致区间是( )
的零点所在的大致区间是( )
A. | B. | C. | D.  |
已知函数 对任意
对任意 都有
都有 ,若
,若 的图象关于直线
的图象关于直线 对称,且
对称,且 ,则
,则
| A.2 | B.3 | C.4 | D.0 |