Question

已知二面角α-l-β的平面角为θ，PA⊥α，PB⊥β，A、B为垂足，且PA=4，PB=5，点A、B到棱l的距离分别为x，y，当θ变化时，点（x，y）的轨迹是下列图形中的（ ）
A．
B．
C．
D．

Answer 1

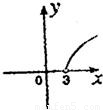
【答案】分析：利用直角三角形的勾股定理得到（x，y）满足的方程，x，y的实际意义得到x，y都大于0据双曲线方程得到（x，y）的轨迹．
解答：解：∵PA⊥α，PB⊥β，
∴PB²+y²=PA²+x²
∵PA=4，PB=5
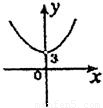
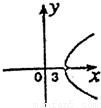
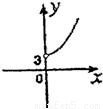
∴x²-y²=9其中x＞0，y＞0
故（x，y）轨迹为双曲线的右上支
故选D
点评：本题考查直角三角形的勾股定理、考查双曲线方程的特点．