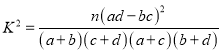题目内容
【题目】动圆M与圆(x﹣1)2+y2=1相外切且与y轴相切,则动圆M的圆心的轨迹记C,
(1)求轨迹C的方程;
(2)定点A(3,0)到轨迹C上任意一点的距离|MA|的最小值;
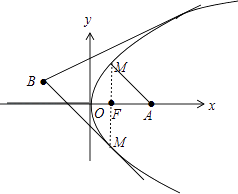
(3)经过定点B(﹣2,1)的直线m,试分析直线m与轨迹C的公共点个数,并指明相应的直线m的斜率k是否存在,若存在求k的取值或取值范围情况[要有解题过程,没解题方程只有结论的只得结论分].
【答案】
(1)解:设动圆圆心M的坐标为(x,y),则 ![]() ,
,
∴(x﹣1)2+y2=x2+2|x|+1,
当x<0时,y=0;当x≥0时,y2=4x
(2)解:如图,由图可知,M到轨迹C上的点与A的距离最小,则M在抛物线y2=4x上,
设M(x,y),则|MA|= ![]() =
= ![]() =
= ![]() .
.
∴当x=1,即M(1,±2)时,|MA|的最小值为2 ![]()
(3)解:设过B与抛物线y2=4x相切的直线方程为y﹣1=k(x+2),即y=kx+2k+1,
联立 ![]() ,得k2x2+(4k2+2k﹣4)x+4k2+4k+1=0.
,得k2x2+(4k2+2k﹣4)x+4k2+4k+1=0.
由△=(4k2+2k﹣4)2﹣4k2(4k2+4k+1)=0,解得:k=﹣1或k= ![]() .
.
∴当直线m的斜率k不存在时或斜率存在为0时或直线m的斜率k∈( ![]() ,+∞)∪(﹣∞,﹣1)时,m与C有1个交点;
,+∞)∪(﹣∞,﹣1)时,m与C有1个交点;
当直线m的斜率为k=﹣1或k= ![]() 或k∈[﹣
或k∈[﹣ ![]() ,0)时,m与C有2个交点;
,0)时,m与C有2个交点;
当直线m的斜率k∈(0, ![]() )∪(﹣1,﹣
)∪(﹣1,﹣ ![]() )时,m与C有3个交点.
)时,m与C有3个交点.
【解析】(1)设出动圆圆心M的坐标,利用动圆M与y轴相切且与圆(x﹣1)2+y2=1外切建立方程,化简得答案;(2)设M的坐标,利用两点间的距离公式结合配方法求得定点A(3,0)到轨迹C上任意一点的距离|MA|的最小值;(3)写出过B斜率存在的直线方程,联立直线方程与抛物线方程,由判别式等于0求得k值,再结合图形求得直线m与轨迹C的公共点个数,并分析对应的斜率情况.

【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100 个网箱,测量各箱水产品的产量(单位:kg).其频率分布直方图如下:
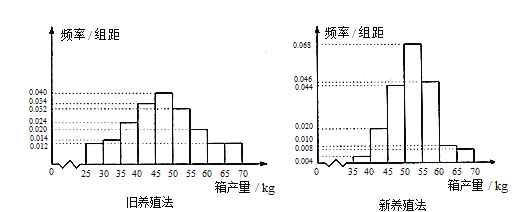
(1)设两种养殖方法的箱产量相互独立,记A表示事件:“旧养殖法的箱产量低于50kg,新养殖法的箱产量不低于50kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50kg | 箱产量≥50kg | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,求新养殖法箱产量的中位数的估计值(精确到0.01).
附: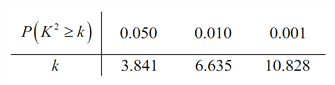 ,
,