题目内容
【题目】某企业生产甲、乙两种产品均需用A，B两种原料，已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获利润分别为3万元、4万元，则该企业每天可获得的最大利润为（ ）
甲 | 乙 | 原料限额 | |
A/吨 | 3 | 2 | 12 |
B/吨 | 1 | 2 | 8 |
A.15万元B.16万元C.17万元D.18万元
【答案】D
【解析】
设该企业每天生产x吨甲产品，y吨乙产品，可获得利润为z万元，根据题意列出x，y满足不等式组和
的表达式，画出可行解域，通过平移直线
找到使得目标函数有最大值时所经过的点的坐标，最后代入求值即可.
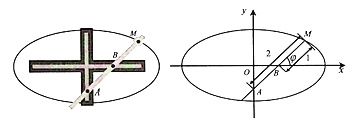
设该企业每天生产x吨甲产品，y吨乙产品，可获得利润为z万元，则z＝3x＋4y，且x，y满足不等式组
画出可行域如图中阴影部分(含边界)所示，
直线z＝3x＋4y过点M时，z＝3x＋4y取得最大值，
由
得
∴M(2，3)，
故z＝3x＋4y的最大值为18，所以该企业每天可获得的最大利润为18万元.
故选：D
【题目】某公司为了对某种商品进行合理定价，需了解该商品的月销售量
（单位：万件）与月销售单价
（单位：元/件）之间的关系，对近
个月的月销售量
和月销售单价
数据进行了统计分析，得到一组检测数据如表所示：
月销售单价 |
|
|
|
|
|
|
月销售量 |
|
|
|
|
|
|
（1）若用线性回归模型拟合与之间的关系，现有甲、乙、丙三位实习员工求得回归直线方程分别为：
，
和
，其中有且仅有一位实习员工的计算结果是正确的．请结合统计学的相关知识，判断哪位实习员工的计算结果是正确的，并说明理由；
（2）若用
模型拟合与之间的关系，可得回归方程为
，经计算该模型和（1）中正确的线性回归模型的相关指数
分别为
和
，请用说明哪个回归模型的拟合效果更好；
（3）已知该商品的月销售额为
（单位：万元），利用（2）中的结果回答问题：当月销售单价为何值时，商品的月销售额预报值最大？（精确到
）
参考数据：
.