题目内容
(2009•枣庄一模)有以下四个命题:
①若x,y∈R,i为虚数单位,且(x-2)i-y=-1+i,则(1+i)x+y的值为-4;
②将函数f(x)=cos(2x+
)+1的图象向左平移
个单位后,对应的函数是偶函数;
③若直线ax+by=4与圆x2+y2=4没有交点,则过点(a,b)的直线与椭圆
+
=1有两个交点;
④在做回归分析时,残差图中残差点分布的带状区域的宽度越窄相关指数越小.
其中所有正确命题的序号为
①若x,y∈R,i为虚数单位,且(x-2)i-y=-1+i,则(1+i)x+y的值为-4;
②将函数f(x)=cos(2x+
| π |
| 3 |
| π |
| 6 |
③若直线ax+by=4与圆x2+y2=4没有交点,则过点(a,b)的直线与椭圆
| x2 |
| 9 |
| y2 |
| 4 |
④在做回归分析时,残差图中残差点分布的带状区域的宽度越窄相关指数越小.
其中所有正确命题的序号为
①③
①③
.分析:①利用复数的四则运算进行求值.②利用三角函数的图象和性质判断.③利用直线与圆的位置关系判断.④利用回归分析的知识进行判断.
解答:解:①由(x-2)i-y=-1+i,得x-2=1且-y=-1,解得x=3,y=1.所以x+y=4,
所以(1+i)x+y=(1+i)4=(2i)2=-4,所以①正确.
②将函数f(x)=cos(2x+
)+1的图象向左平移
个单位后,得到函数为y=cos[2(x+
)+
]+1=cos(2x+
)+1,
此时函数不是偶函数,所以②错误.
③因为直线ax+by=4与圆x2+y2=4没有交点,所以圆心到直线的距离d=
>2,即
<2,即点P(a,b)到原点的距离|OP|<2,
因为由椭圆的方程可知,a=2,所以点P(a,b)在椭圆的内部,所以过点(a,b)的直线与椭圆
+
=1有两个交点,所以③正确.
④可用残差图判断模型的拟合效果,残差点比较均匀地落在水平的带状区域中,说明这样的模型比较合适.带状区域的宽度越窄,说明模型的拟合精度越高.
则对应相关指数越大,所以④错误.
故答案为:①③.
所以(1+i)x+y=(1+i)4=(2i)2=-4,所以①正确.
②将函数f(x)=cos(2x+
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
此时函数不是偶函数,所以②错误.
③因为直线ax+by=4与圆x2+y2=4没有交点,所以圆心到直线的距离d=
| |4| | ||
|
| a2+b2 |
因为由椭圆的方程可知,a=2,所以点P(a,b)在椭圆的内部,所以过点(a,b)的直线与椭圆
| x2 |
| 9 |
| y2 |
| 4 |
④可用残差图判断模型的拟合效果,残差点比较均匀地落在水平的带状区域中,说明这样的模型比较合适.带状区域的宽度越窄,说明模型的拟合精度越高.
则对应相关指数越大,所以④错误.
故答案为:①③.
点评:本题主要考查命题的真假判断,涉及的知识点较多,综合性较强,要求熟练掌握相关的知识.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
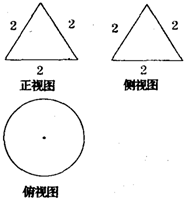 (2009•枣庄一模)一个几何体的三视图如图所示,则该几何体外接球的表面积为( )
(2009•枣庄一模)一个几何体的三视图如图所示,则该几何体外接球的表面积为( )