题目内容
(2009•枣庄一模)设复数z的共轭复数是
,若复数z1=3+4i,z2=t+i,且z1•
是实数,则实数t=( )
. |
| z |
. |
| z2 |
分析:首先求出复数z2=t+i的共轭复数,代入z1•
整理后由虚部等于0可求t得值.
. |
| z2 |
解答:解:由z2=t+i,得
=t-i,
又z1=3+4i,所以z1•
=(3+4i)(t-i)=(3t+4)+(4t-3)i.
又z1•
是实数,所以4t-3=0,解得t=
.
故选A.
. |
| z2 |
又z1=3+4i,所以z1•
. |
| z2 |
又z1•
. |
| z2 |
| 3 |
| 4 |
故选A.
点评:本题考查了复数代数形式的乘除运算,考查了复数是实数的条件,一个复数是实数,当且仅当虚部等于0,是基础题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
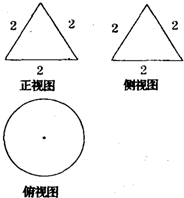 (2009•枣庄一模)一个几何体的三视图如图所示,则该几何体外接球的表面积为( )
(2009•枣庄一模)一个几何体的三视图如图所示,则该几何体外接球的表面积为( )