题目内容
函数f(x)=2-|x|的值域是 ________.
(0,1]
分析:函数f(x)=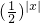 ,个偶函数,在(-∞,0)上增函数,在[0,+∞)上是个减函数,x=0时,有最大值1.
,个偶函数,在(-∞,0)上增函数,在[0,+∞)上是个减函数,x=0时,有最大值1.
解答:函数f(x)=2-|x|=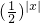 ,
,
此函数是个偶函数,在(-∞,0)上增函数,在[0,+∞)上是个减函数,
故x=0时,有最大值1,
又由指数函数的性质知,f(x)>0,
故函数的值域(0,1],
故答案为 (0,1].
点评:本题考查指数函数的单调性及单调区间、值域,体现了转化的数学思想.
分析:函数f(x)=
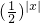 ,个偶函数,在(-∞,0)上增函数,在[0,+∞)上是个减函数,x=0时,有最大值1.
,个偶函数,在(-∞,0)上增函数,在[0,+∞)上是个减函数,x=0时,有最大值1.解答:函数f(x)=2-|x|=
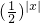 ,
,此函数是个偶函数,在(-∞,0)上增函数,在[0,+∞)上是个减函数,
故x=0时,有最大值1,
又由指数函数的性质知,f(x)>0,
故函数的值域(0,1],
故答案为 (0,1].
点评:本题考查指数函数的单调性及单调区间、值域,体现了转化的数学思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目