题目内容
已知 >0,函数f(x)=sin(
>0,函数f(x)=sin( x+
x+ )在(
)在( ,
, )上单调递减,则
)上单调递减,则 的取值范围是( )
的取值范围是( )
A.[ , ,  ] ] |
B.[ , ,  ] ] |
C.[0, ] ] |
D. |
A
解析法一:赋值排除法 =1时,令Z=
=1时,令Z= x+
x+ =x+
=x+ ,当x∈(
,当x∈( ,
, ) 时,Z∈[
) 时,Z∈[ ,
, ],此时sinZ单调递减,
],此时sinZ单调递减,
符合题意,排除B,C =2时,令Z=
=2时,令Z= x+
x+ =2x+
=2x+ ,当x∈(
,当x∈( ,
, ) 时,Z∈[
) 时,Z∈[ ,
,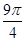 ],此时sinZ单调递减不成立,不符合题意,排除D
],此时sinZ单调递减不成立,不符合题意,排除D
法二:直接法 令Z= x+
x+
∵sinZ的单调递减区间为[ ,
, ]( k∈Z),
]( k∈Z),
即 ≤Z≤
≤Z≤ ( k∈Z), 解之得
( k∈Z), 解之得 ≤x≤
≤x≤ (k∈Z)
(k∈Z)
由题意知: ≤
≤ 且
且 ≥
≥ (k∈Z)
(k∈Z)
即 (k∈Z)
(k∈Z)
∵ ,∴k<
,∴k<
又 >0,∴k=0,即
>0,∴k=0,即

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若函数 在区间
在区间 上存在一个零点,则实数
上存在一个零点,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. 或 或 | D. |
函数 的定义域是( )
的定义域是( )
A.(- ,1) ,1) | B.(- ,+∞) ,+∞) | C.(- , , ) ) | D.(-∞,-  ) ) |
已知 其导函数
其导函数 的图象如图,则函数
的图象如图,则函数 的极小值是( )
的极小值是( )
A. |
B. |
C. |
| D.c |
下列函数中,既是偶函数,又是在区间(0,+∞)上单调递减的函数是( )
A. |
B.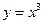 |
C. |
D. |
函数 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时,
时, ,则函数
,则函数 的零点为( )
的零点为( )
| A.2 |
B. |
| C.3 |
| D.0 |
已知f(x)是定义在R上的以3为周期的偶函数,若f(1)<1,f(5)=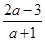 ,则实数a的取值范围为()
,则实数a的取值范围为()
| A.-1<a<4 | B.-2<a<1 | C.-1<a<2 | D.-1<a<0 |
 的图象大致是( )
的图象大致是( )
 的图像如左图,则导函数
的图像如左图,则导函数 的图像可能是下图中的()
的图像可能是下图中的()